第四届山东省省赛题解

A - Problem A:Rescue The Princess

题型：

几何

题意：

给你等边三角形的两个点A和B，求第三个点C的坐标；

且ABC是逆时针的；

题解：

因为要求ABC是逆时针的，所以可以直接用B绕A逆时针旋转60°；

这里有个通用的公式，证明稍微复杂，可以加到模板里以备不时之需：

点（x1，y1）绕点（x2，y2）逆时针旋转a角度后新的坐标（X，Y）为:

X=(x1-x2)*cos(a)-(y1-y2)*sin(a)+x2;

Y=(x1-x2)*sin(a)+(y1-y2)*cos(a)+y2;

如果直接按照题意的等边三角形的情况去画图推导也可以推导出来，不过这个公式比较普适。

#include <stdio.h>
#include <iostream>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <algorithm>

using namespace std;
int main() {
    int t;
    scanf("%d", &t);
    while(t--){
        double x1,x2,x3,y1,y2,y3;
        scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
        double dx=x2-x1,dy=y2-y1;
        x3=dx/2-dy*sqrt(3.0)/2+x1;
        y3=dy/2+dx*sqrt(3.0)/2+y1;
        printf("(%.2lf,%.2lf)
",x3,y3);
    }
    return 0;
}

B - Problem B:Thrall’s Dream

题意：

有n个点、m条边，问是否任意两个点都是联通的

题解：

对每一个点进行bfs，记录下所有与其联通的点，若最后所有点互相联通

输出Kalimdor is just ahead，否则输出另一个。

Ps：两个点联通不需要相邻

Pss：若用邻接矩阵储存会超时，此处使用vector优化

#include <stdio.h>
#include <iostream>
#include <string.h>
#include <queue>
#include <vector>
using namespace std;
#define N 2020
int vis[N],ans[N][N];
vector <int> path[N];
int m,n;
void bfs(int s)
{
    memset(vis,0,sizeof(vis));
    vis[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int first=q.front();
        q.pop();
        for(int i=0; i<path[first].size(); i++)
        {

            int t=path[first][i];
            if(vis[t])
                continue;
            ans[s][t]=1;
            q.push(t);
            vis[t]=1;

        }
    }
}
bool f()
{

    for(int i=1; i<=n; i++)
        for(int j=i+1; j<=n; j++)
            if(!ans[i][j]&&!ans[j][i])
                return 0;
    return 1;
}
int main()
{
    int cases;
    cin >> cases;
    for(int j=1; j<=cases; j++)
    {
        int a,b;
        cin >> n >> m;
        for(int i=0; i<N; i++)
            path[i].clear();
        memset(ans,0,sizeof(ans));
        while(m--)
        {
            cin >> a >> b;
            path[a].push_back(b);
        }
        for(int i=1; i<=n; i++)
            bfs(i);
        if(f())
            printf("Case %d: Kalimdor is just ahead
",j);
        else
            printf("Case %d: The Burning Shadow consume us all
",j);
    }
    return 0;
}

C - Problem C:A^X mod P

题型：

大幂的分解和、打表

题意：

给出七个整数n，A，K，a，b，m，P和函数f（x），定义如下：

f（x）= K，x = 1

f（x）=（a * f（x-1）+ b）％m，x> 1

计算：

( A^(f(1)) + A^(f(2)) + A^(f(3)) + ...... + A^(f(n)) ) % P.

题解：

用快速幂会超时，所以用数组存储f(x)的值，计算的时候直接去取。

将f(x)分解为a*k+b，再利用x^(a+b)=x^a * x^b，即可。

#include <stdio.h>
#define MAX 3333
long long t,n,A,K,a,b,m,P;
long long L1[MAX+10], L2[MAX+10];
void L()
{
    int i;
    long long res;
    L1[0] = 1;
    for(i = 1; i <= MAX; i++)
        L1[i] = (L1[i-1]*A)%P;
    L2[0] = 1;
    for(i = 1; i <= MAX; i++)
        L2[i] = (L2[i-1]*L1[MAX])%p;

}
int main(void)
{
    int cas = 1;
    long long i,sum;
    scanf("%lld", &t);
    while(t--){
        sum = 0;
        scanf("%ld%lld%lld%lld%lld%lld%lld", &n,&A,&K,&a,&b,&m,&p);
        for(i = 1; i <= n; i++){
            sum = (sum+(L1[K%MAX]*L2[K/MAX])%p)%p;
            K = (a*K+b)%m;
        }
        printf("Case #%d: %lld
", cas, sum);
        cas++;
    }
    return 0;
}

E - Problem E:Mountain Subsequences

题意：

求满足以某元素为中心，左边递增右边递减的子串数目

Ps：最小长度为3，切中心元素左右至少各一个元素

Pps：aaba中，前两个a是不同的有a1ba、a2ba两个答案

题解：

求出每个字符为中心的左侧递增子序列和右侧递减子序列

然后左右相乘求和

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
#define MAX 100010
char ch[MAX];
int n,a[MAX],dp1[MAX],dp2[MAX],dp[MAX];
int main()
{
    while(cin >> n)
    {
        getchar();
        scanf("%s", ch);
        for(int i = 0; i < n; i++)
            a[i]=ch[i]-'a';
        memset(dp1, 0, sizeof(dp1));
        memset(dp2, 0, sizeof(dp2));
        memset(dp, 0, sizeof(dp));
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < a[i]; j++)
                dp1[i] = (dp1[i]+dp[j])%2012;
            dp[a[i]] = (dp[a[i]]+dp1[i]+1)%2012;
        }
        memset(dp, 0, sizeof(dp));
        for(int i = n-1; i >= 0; i--)
        {
            for(int j = 0; j < a[i]; j++)
                dp2[i] = (dp2[i]+dp[j])%2012;
            dp[a[i]] = (dp[a[i]]+dp2[i]+1)%2012;
        }
        int ans = 0;
        for(int i = 0; i < n; i++)
            ans = (ans+dp1[i]*dp2[i])%2012;
        cout << ans << endl;
    }
    return 0;
}

F - Problem F:Alice and Bob

题型：

规律  二进制

题意：

求：

(a0*x^(2^0)+1) * (a1 * x^(2^1)+1)*.......*(an-1 * x^(2^(n-1))+1)

展开式中x^q的系数。

题解：

首先，看到数据范围就可以猜测这应该是道规律题。

然后，观察x的指数：2^0  2^1 ... 2^(n-1)，可以联想到二进制

将样例3、4写成二进制的形式

3  =  1   1

      a1  a0

4  =  1   0   0

      a2  a1  a0

另外发现展开式中的x的指数没有相同的项，即不会合并同类项

规律：结果为二进制为1的位置对应的系数相乘

#include <stdio.h>
int main(void)
{
    int t,n,q;
    int i,j,k;
    int s[55];
    long long res,p;
    scanf("%d", &t);
    while(t--){
        scanf("%d", &n);
        for(i = 0; i < n; i++)
            scanf("%d", s+i);
        scanf("%d", &q);
        while(q--){
            j = 0;
            res = 1;
            scanf("%lld", &p);
            while(p){
                if(j >= n){
                    res = 0;
                    break;
                }
                if(p%2)
                    res = (res * s[j]) % 2012;
                j++;
                p /= 2;
            }
            printf("%lld
", res);
        }
    }
    return 0;
}

I - Problem I:The number of steps

题型：

概率dp/数学期望

题意：

一个金字塔，从顶端往下走，规定只能向左、左下、右下走，给你对应的概率，求从顶端走到最底层的左下角那个房间的期望。

输入层数n还有五个浮点数a,b,c,d,e；

当只有一个房间的时候，概率是1；

当没有左，只有左下和右下的时候，概率是a和b；  a+b=1;

当左，左下，右下都有的时候，概率是c,d,e；          c+d+e=1;

题解：

综合思想是：从左下角往顶端倒推；

期望基本公式：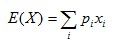

期望基本性质：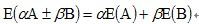

#include <stdio.h>
#include <iostream>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <algorithm>

using namespace std;
int main() {
    int n;
    double a,b,c,d,e;
    while(scanf("%d", &n)&&n){
        scanf("%lf%lf%lf%lf%lf", &a, &b, &c, &d, &e);
        double dp[100][100]={0};
        for(int i=n-1;i>0;i--){
            dp[n][i]+=dp[n][i+1]+1;
        }
        for(int i=n-1;i>0;i--){
            dp[i][i]+=a*(dp[i+1][i+1]+1)+b*(dp[i+1][i]+1);//此处是计算只有左下右下那种情况的；
            for(int j=i-1;j>0;j--)
                dp[i][j]+=c*(dp[i+1][j+1]+1)+d*(dp[i+1][j]+1)+e*(dp[i][j+1]+1);//此处是计算左，左下，右下情况的；
        }
        printf("%.2lf
",dp[1][1]);
    }
    return 0;
}

J - Problem J:Contest Print Server

题型：

水题模拟

题意：

一开始打印机能打印s张，每一队有需要打印的纸张数目，如果该队打印完则到下一队，如果该队打印过程中纸张用完，则新的纸张会到达，而新纸张的数目是在原纸张本来数目上进行s=(s*x+y)%mod的运算，新纸张来后，打印序列必须从0开始，输出此过程；

题解：

直接模拟；

Pｓ：０张也是可以输出的；

#include <stdio.h>  
#include <string.h>  
#include <algorithm>  
using namespace std;  
  
struct node  
{  
    char name[30];  
    int num;  
} team[105];  
  
int main()  
{  
    int t,n,s,x,y,mod,i,j,cnt;  
    scanf("%d",&t);  
    while(t--)  
    {  
        scanf("%d%d%d%d%d",&n,&s,&x,&y,&mod);  
        for(i = 1; i<=n; i++)  
            scanf("%s request %d pages",team[i].name,&team[i].num);  
            cnt = s;  
        for(i = 1; i<=n; i++)  
        {  
            while(1)  
            {  
                if(team[i].num<=cnt)  
                {  
                    printf("%d　pages for %s
",team[i].num,team[i].name);  
                    cnt-=team[i].num;  
                    break;  
                }  
                else  
                {  
                    printf("%d pages for %s
",cnt,team[i].name);  
                    s = (s*x+y)%mod;  
                        cnt = s;  
                }  
            }  
        }  
        printf("
");  
    }  
  
    return 0;  
}