hdu 5134 Highway

题意是：你当前距离高速公路D米，你在高速公路的行驶速度为v1,在其他地方行驶速度是v0  (v1>v0)，然后问你在T秒能到达的区域的面积

我们可以在高速公路上找到一点p，只考虑上半个平面（下半个是一样的）,使得 从 now 到 p，然后在从 p 沿着高速公路向上走到达一个最远距离，可以用三分得到这个点

而且此时 now -> p的时间会小于等于 now -> O + O ->p 证明如下：

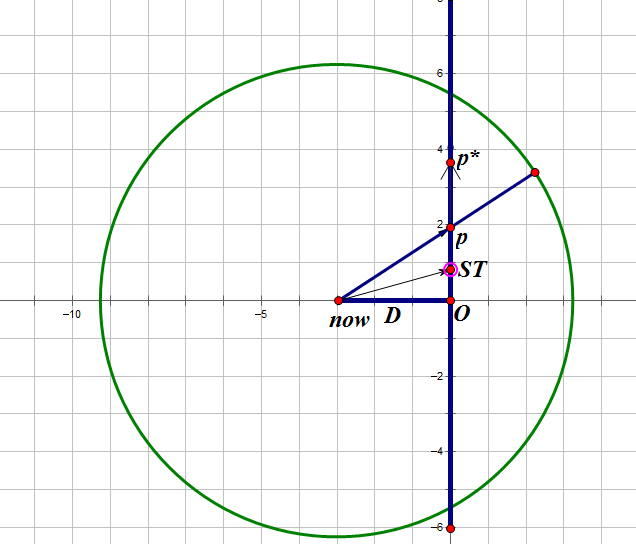
 因为肯定存在一点ST,使得 now->ST 的时间等于 now->O + O->ST

假设 p点在ST的上面，now->p 的时间会大于 now-ST + ST->p 的时间，所以走now - >ST +ST->p 的路径会更优，所以 p点一定在 O到ST 这段里面

所以在从now 到  O到p  这一段中的点 p1，直接从now->p1所花费的时间会最少，然后在以p1为出发点所能到达的区域就是以 p1为圆心的圆，并且这个圆会与大圆相内切

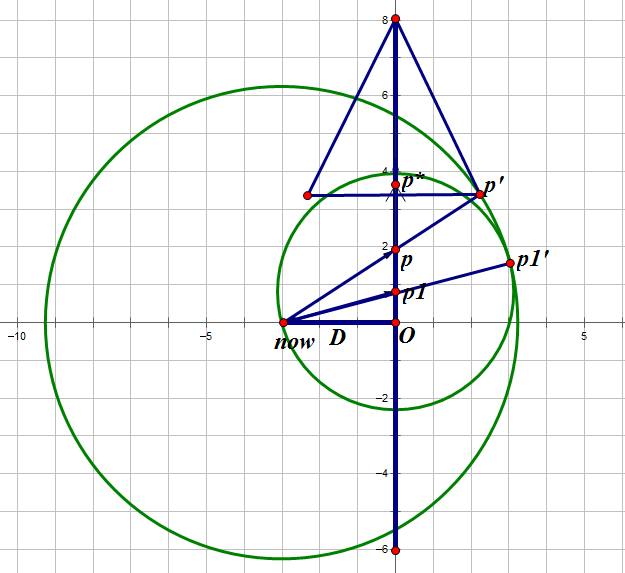
对于p点上面部分的点，以它们为圆心的圆 会形成一个三角形（证明略）

所以我们的答案就是 ans = 大圆面积 + 2*三角形面积 - 2*三角形与圆的面积交

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long LL;

const double PI = acos(-1.0);
const double EPS = 1e-7;

inline int sgn(double x) {
    return (x > EPS) - (x < -EPS);
}

struct Point {
    double x, y;
    Point() {}
    Point(double x, double y): x(x), y(y) {}
    void read() {
        scanf("%lf%lf", &x, &y);
    }
    double angle() {
        return atan2(y, x);
    }
    Point operator + (const Point &rhs) const {
        return Point(x + rhs.x, y + rhs.y);
    }
    Point operator - (const Point &rhs) const {
        return Point(x - rhs.x, y - rhs.y);
    }
    Point operator * (double t) const {
        return Point(x * t, y * t);
    }
    Point operator / (double t) const {
        return Point(x / t, y / t);
    }
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    double length() const {
        return sqrt(x * x + y * y);
    }
    Point unit() const {            //单位向量
        double l = length();
        return Point(x / l, y / l);
    }
};
double cross(Point a,Point b) {
    return a.x * b.y - a.y * b.x;
}
double cross(Point a,Point b,Point c){
    return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x);
}
double xml(Point a,Point b,Point c){
    return (a.x-c.x)*(b.x-c.x)+(a.y-c.y)*(b.y-c.y);
}
double sqr(double x) {
    return x * x;
}
double dist(const Point &p1, const Point &p2) {
    return (p1 - p2).length();
}
double sdist(Point a,Point b){
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
//向量 op 逆时针旋转 angle
Point rotate(const Point &p, double angle, const Point &o = Point(0, 0)) {
    Point t = p - o;
    double x = t.x * cos(angle) - t.y * sin(angle);
    double y = t.y * cos(angle) + t.x * sin(angle);
    return Point(x, y) + o;
}
Point line_inter(Point A,Point B,Point C,Point D){ //直线相交交点
        Point ans;
        double a1=A.y-B.y;
        double b1=B.x-A.x;
        double c1=A.x*B.y-B.x*A.y;

        double a2=C.y-D.y;
        double b2=D.x-C.x;
        double c2=C.x*D.y-D.x*C.y;

        ans.x=(b1*c2-b2*c1)/(a1*b2-a2*b1);
        ans.y=(a2*c1-a1*c2)/(a1*b2-a2*b1);
        return ans;
}
Point p_to_seg(Point p,Point a,Point b){        //点到线段的最近点
    Point tmp=p;
    tmp.x+=a.y-b.y;
    tmp.y+=b.x-a.x;
    if(cross(a-p,tmp-p)*cross(b-p,tmp-p)>0) return dist(p,a)<dist(p,b)?a:b;
    return line_inter(p,tmp,a,b);
}
void line_circle(Point c,double r,Point a,Point b,Point &p1,Point &p2){
    Point tmp=c;
    double t;
    tmp.x+=(a.y-b.y);//求垂直于ab的直线
    tmp.y+=(b.x-a.x);
    tmp=line_inter(tmp,c,a,b);
    t=sqrt(sqr(r)-sqr( dist(c,tmp)))/dist(a,b); //比例
    p1.x=tmp.x+(b.x-a.x)*t;
    p1.y=tmp.y+(b.y-a.y)*t;
    p2.x=tmp.x-(b.x-a.x)*t;
    p2.y=tmp.y-(b.y-a.y)*t;
}
struct Region {
    double st, ed;
    Region() {}
    Region(double st, double ed): st(st), ed(ed) {}
    bool operator < (const Region &rhs) const {
        if(sgn(st - rhs.st)) return st < rhs.st;
        return ed < rhs.ed;
    }
};
struct Circle {
    Point c;
    double r;
    vector<Region> reg;
    Circle() {}
    Circle(Point c, double r): c(c), r(r) {}
    void read() {
        c.read();
        scanf("%lf", &r);
    }
    void add(const Region &r) {
        reg.push_back(r);
    }
    bool contain(const Circle &cir) const {
        return sgn(dist(cir.c, c) + cir.r - r) <= 0;
    }
    bool intersect(const Circle &cir) const {
        return sgn(dist(cir.c, c) - cir.r - r) < 0;
    }
};
void intersection(const Circle &cir1, const Circle &cir2, Point &p1, Point &p2) {   //两圆相交 交点
    double l = dist(cir1.c, cir2.c);                            //两圆心的距离
    double d = (sqr(l) - sqr(cir2.r) + sqr(cir1.r)) / (2 * l);  //cir1圆心到交点直线的距离
    double d2 = sqrt(sqr(cir1.r) - sqr(d));                     //交点到 两圆心所在直线的距离
    Point mid = cir1.c + (cir2.c - cir1.c).unit() * d;
    Point v = rotate(cir2.c - cir1.c, PI / 2).unit() * d2;
    p1 = mid + v, p2 = mid - v;
}
Point calc(const Circle &cir, double angle) {
    Point p = Point(cir.c.x + cir.r, cir.c.y);
    return rotate(p, angle, cir.c);
}
const int MAXN = 1010;
Circle cir[MAXN],cir2[MAXN];
bool del[MAXN];
int n;
double get_area(Circle* cir,int n) {            //多个圆的相交面积
    double ans = 0;
    memset(del,0,sizeof(del));
    for(int i = 0; i < n; ++i) {
        for(int j = 0; j < n; ++j) if(!del[j]) {                //删除被包含的圆
            if(i == j) continue;
            if(cir[j].contain(cir[i])) {
                del[i] = true;
                break;
            }
        }
    }
    for(int i = 0; i < n; ++i) if(!del[i]) {
        Circle &mc = cir[i];
        Point p1, p2;
        bool flag = false;
        for(int j = 0; j < n; ++j) if(!del[j]) {
            if(i == j) continue;
            if(!mc.intersect(cir[j])) continue;
            flag = true;
            intersection(mc, cir[j], p1, p2);                   //求出两圆的交点
            double rs = (p2 - mc.c).angle(), rt = (p1 - mc.c).angle();
            if(sgn(rs) < 0) rs += 2 * PI;
            if(sgn(rt) < 0) rt += 2 * PI;
            if(sgn(rs - rt) > 0) mc.add(Region(rs, PI * 2)), mc.add(Region(0, rt)); //添加相交区域
            else mc.add(Region(rs, rt));
        }
        if(!flag) {
            ans += PI * sqr(mc.r);
            continue;
        }
        sort(mc.reg.begin(), mc.reg.end());                 //对相交区域进行排序
        int cnt = 1;
        for(int j = 1; j < int(mc.reg.size()); ++j) {
            if(sgn(mc.reg[cnt - 1].ed - mc.reg[j].st) >= 0) {   //如果有区域可以合并，则合并
                mc.reg[cnt - 1].ed = max(mc.reg[cnt - 1].ed, mc.reg[j].ed);
            } else mc.reg[cnt++] = mc.reg[j];
        }
        mc.add(Region());
        mc.reg[cnt] = mc.reg[0];
        for(int j = 0; j < cnt; ++j) {
            p1 = calc(mc, mc.reg[j].ed);
            p2 = calc(mc, mc.reg[j + 1].st);
            ans += cross(p1, p2) / 2;                           //
            double angle = mc.reg[j + 1].st - mc.reg[j].ed;
            if(sgn(angle) < 0) angle += 2 * PI;
            ans += 0.5 * sqr(mc.r) * (angle - sin(angle));      //弧所对应的的面积
        }
    }
    return ans;
}
double two_cir(Circle t1,Circle t2){            //两个圆的相交面积
    if(t1.contain(t2)||t2.contain(t1))    return PI * sqr(min(t2.r,t1.r));
    if(!t1.intersect(t2)) return 0;
    double ans=0,len=dist(t1.c,t2.c);
    double x=(sqr(t1.r)+sqr(len)-sqr(t2.r))/(2*len);
    double angle1=acos(x/t1.r),angle2=acos((len-x)/t2.r);
    ans=sqr(t1.r)*angle1+sqr(t2.r)*angle2-len*t1.r*sin(angle1);    // 两个扇形 减去一个四边形面积
    return ans;
}
double EP=0;
double triangle_circle(Point a,Point b,Point c,double r){//三角形与圆交
    double A,B,C,x,y,tS;
    A=dist(b,c);
    B=dist(a,c);
    C=dist(b,a);
    if(A<r&&B<r)
    return cross(a,b,c)/2;
    else if(A<r&&B>=r){
        x=(xml(a,c,b)+sqrt(r*r*C*C-cross(a,c,b)*cross(a,c,b)))/C;
        tS=cross(a,b,c)/2;
        return asin(tS*(1-x/C)*2/r/B*(1-EP))*r*r/2+tS*x/C;
    }
    else if(A>=r&&B<r){
        y=(xml(b,c,a)+sqrt(r*r*C*C-cross(b,c,a)*cross(b,c,a)))/C;
        tS=cross(a,b,c)/2;
        return asin(tS*(1-y/C)*2/r/A*(1-EP))*r*r/2+tS*y/C;
    }
    else if(fabs(cross(a,b,c))>=r*C||xml(b,c,a)<=0||xml(a,c,b)<=0){
        if(xml(a,b,c)<0)
            if(cross(a,b,c)<0)
                return (-acos(-1.0)-asin(cross(a,b,c)/A/B*(1-EP)))*r*r/2;
            else return (acos(-1.0)-asin(cross(a,b,c)/A/B*(1-EP)))*r*r/2;
        else return asin(cross(a,b,c)/A/B*(1-EP))*r*r/2;
    }
    else{
        x=(xml(a,c,b)+sqrt(r*r*C*C-cross(a,c,b)*cross(a,c,b)))/C;
        y=(xml(b,c,a)+sqrt(r*r*C*C-cross(b,c,a)*cross(b,c,a)))/C;
        tS=cross(a,b,c)/2;
        return (asin(tS*(1-x/C)*2/r/B*(1-EP))+asin(tS*(1-y/C)*2/r/A*(1-EP)))*r*r/2+tS*((y+x)/C-1);
    }
}
Point pt1[5100],cter;
double r;
Point three_P_mincover(Point a,Point b,Point c){ //三角形的外接圆
    Point ret;
    double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;
    double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;
    double d=a1*b2-a2*b1;
    ret.x=a.x+(c1*b2-c2*b1)/d;
    ret.y=a.y+(a1*c2-a2*c1)/d;
    return ret;
}
void min_circle_cover(){                //点的最小覆盖
    random_shuffle(pt1,pt1+n);
     cter=pt1[0];
     r=0;
     for(int i=1;i<n;i++){
        if(dist(cter,pt1[i])-r>EPS){
            cter=pt1[i];
            r=0;
            for(int j=0;j<i;j++){
                if(dist(cter,pt1[j])-r>EPS){
                    cter=(pt1[i]+pt1[j])/2.0;
                    r=dist(cter,pt1[i]);
                    for(int k=0;k<j;k++){
                        if(dist(cter,pt1[k])-r>EPS){
                            cter=three_P_mincover(pt1[i],pt1[j],pt1[k]);
                            r=dist(cter,pt1[i]);
                        }
                    }
                }
            }
        }
     }
}
int main(){
    #ifndef ONLINE_JUDGE
    freopen("input.txt","r",stdin);
    #endif // ONLINE_JUDGE
    double v0,v1,D,T;
    int cas=0;
    Point cter;
    while(scanf("%lf%lf%lf%lf",&v0,&v1,&D,&T)!=EOF){
        double p_t,l=D/v0,r=T,mid,mmid;
        cter=Point(-D,0);
        if(D>=v0*T){
            printf("Case %d: %.8f
",++cas,PI*v0*v0*T*T);
            continue;
        }
        for(int i=0;i<100;i++){
            mid=(l+r)/2;
            mmid=(r+mid)/2;
            double len1,len2;
            len1=sqrt(v0*mid*v0*mid-D*D)+v1*(T-mid);
            len2=sqrt(v0*mmid*v0*mmid-D*D)+v1*(T-mmid);
            if(len1>len2) r=mmid;
            else l=mid;
        }
        p_t=(l+r)/2;
        double x1,y1,y;
        x1=T/p_t*D-D;
        y1=sqrt(v0*T*v0*T-(x1+D)*(x1+D));
        y=sqrt(v0*p_t*v0*p_t-D*D)+v1*(T-p_t);
        double ans=0,tmp=0;
        Point a,b,c;
        a=Point(x1,y1);
        b=Point(0,y);
        c=Point(-x1,y1);
        tmp+=triangle_circle(a,b,cter,v0*T);
        tmp+=triangle_circle(b,c,cter,v0*T);
        tmp+=triangle_circle(c,a,cter,v0*T);
        tmp=fabs(tmp);
        ans=PI*v0*v0*T*T+cross(a-c,b-c);
        ans-=tmp*2;
        printf("Case %d: %.8f
",++cas,ans);
    }
}