梯度下降算法/最速下降算法: 快速寻找函数局部极小值
- 监督学习
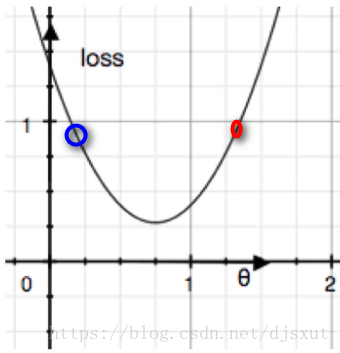
损失函数的导数称为梯度,若对损失函数的参数θ求偏导,则这个偏导数代表着损失函数在该参数θ下各点的斜率;
目标就是让损失能尽可能的小,希望取到损失函数的最小值,可以通过梯度函数得到损失函数上各点的斜率,然后逐步更新参数从而满足要求的这种方法就是梯度下降!
对于L2损失,参数θ对应的梯度函数如下:
若参数θ上某一点对应梯度为正值(上图红点),此时应该减小θ,即加上一个负数,从而降低loss;
若参数θ上某一点对应梯度为负值(上图蓝点),此时应该增加θ,即给θ加上一个正数来降低loss;
以L2损失为例,可以定义损失函数和梯度更新函数如下:

依然使用L2损失,使用上面的结果,在bias恒为0的情况下,在下面例子中,可以通过持续的权重更新最终使的 y = f(x) = t。从下面例子中也可以看出,较小的学习率(learning rate)虽然会使得求解过程稍慢,但最后求得的目标函数较学习率(学习率为1, w=[2, -2])较大的目标函数更“精准”;
所以,后续学习率可按下面这种方法来尝试进行迭代更新:
1. 初始化一个相对较小的,经验的学习率,如 0.1, 0.001等;
2. 若学习率导致梯度爆炸,可以适当减小学习率(可减小为原来的1/10, 1/100等);
3. 若目标函数收敛,可适当增大学习率(可增大为原来的10, 100等);
4. 通过对2/3持续验证优化,得到一个合适的学习率值;

总结:
求函数f(x)的最小值的梯度下降方法:
- 给定初始值x
- 更新x,使得f(x)越来越小 
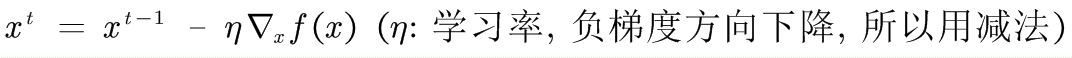
- 直到收敛到/达到预先设定的最大迭代次数
可能带来的问题:
- 学习率太小,收敛速度就会较慢,可能得到的是局部最小值;这个时候可以随机选择多个初始值,从得到的多个局部最小值中挑选最小的那个值作为全局极小值(对于凸函数(二阶导数 > 0),局部极小值即为全局最小值)。
- 学习率太大,可能引起梯度爆炸现象(overshoot the minimum)!