经常听说线性回归(Linear Regression) 到底什么才是线性,什么才是回归?
有学者说,线性回归模型是一切模型之母。所以,我们的机器学习之旅,也将从这个模型开始!
建立回归模型的好处:随便给一个x,就能通过模型算出y,这个y可能和实际值不一样,这个y是对实际值的一个可靠的预测
要想理解线性回归,就得理解下面几个问题:
1、什么是回归?
在几何意义上,回归就是找到一条具有代表性的直线或曲线(高维空间的超平面)来拟合输入数据点和输出数据点!
我查按了很多资料,也没有确切的定义;按我自己的理解给了个定义:
回归 是分析研究变量与变量之间的关系的一种行为,也可以说是回归于事物本来的面目!
一个模型和数据因为回归的存在,可能达到了一种理想化的拟合状态。这么说来,回归就是一种分析手段而已
2、什么是回归分析?
在统计学中,回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
3、回归(预测)与分类的区别
监督学习中,
- 如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),
- 如果预测的变量是连续的,我们称其为回归。
分类和回归的区别在于输出变量的类型:
定量输出(有大概的结果)称为回归,或者说是连续变量预测;
定性输出(有确定的结果)称为分类,或者说是离散变量预测。
举个例子:
预测明天的气温是多少度,这是一个回归任务;
预测明天是阴、晴还是雨,就是一个分类任务。
4、什么是线性回归
一句话总结:线性回归就是在N维空间中找一个形式像直线方程一样的函数来拟合数据而已,找直线的过程就是在做线性回归!
线性回归是利用统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。其表达形式为y = w'x+e,e为误差服从均值为0的正态分布
线性模型:在线性回归中,数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。
5、 目标/损失函数
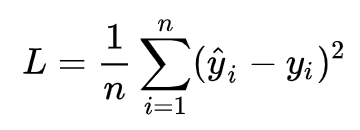
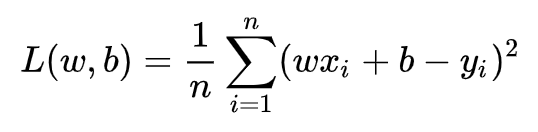

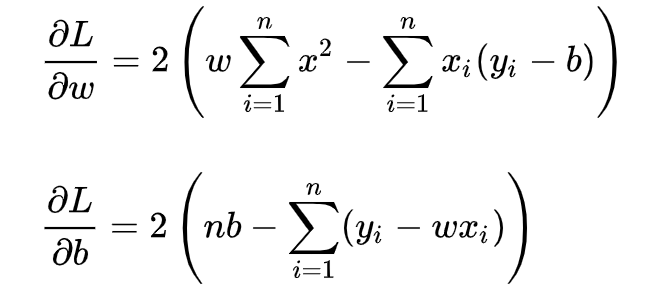

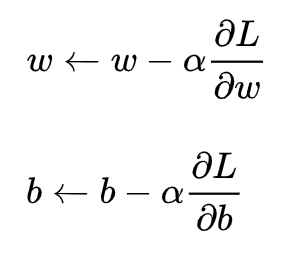
5、线性回归的代码实现?
5.1 简单线性回归

# -*- coding: utf-8 -*- import numpy as np class LinerRegression(object): def __init__(self, learning_rate=0.01, max_iter=100, seed=None): np.random.seed(seed) self.lr = learning_rate self.max_iter = max_iter self.w = np.random.normal(1, 0.1) self.b = np.random.normal(1, 0.1) self.loss_arr = [] def fit(self, x, y): self.x = x self.y = y for i in range(self.max_iter): self._train_step() self.loss_arr.append(self.loss()) # print('loss: {:.3}'.format(self.loss())) # print('w: {:.3}'.format(self.w)) # print('b: {:.3}'.format(self.b)) def _f(self, x, w, b): return x * w + b def predict(self, x=None): if x is None: x = self.x y_pred = self._f(x, self.w, self.b) return y_pred def loss(self, y_true=None, y_pred=None): if y_true is None or y_pred is None: y_true = self.y y_pred = self.predict(self.x) return np.mean((y_true - y_pred)**2) def _calc_gradient(self): d_w = np.mean((self.x * self.w + self.b - self.y) * self.x) d_b = np.mean(self.x * self.w + self.b - self.y) return d_w, d_b def _train_step(self): d_w, d_b = self._calc_gradient() self.w = self.w - self.lr * d_w self.b = self.b - self.lr * d_b return self.w, self.b
建立 train.py 文件,用于生成模拟数据,并调用 liner_regression.py 中的类,完成线性回归任务:

# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt from liner_regression import * def show_data(x, y, w=None, b=None): plt.scatter(x, y, marker='.') if w is not None and b is not None: plt.plot(x, w*x+b, c='red') plt.show() # data generation np.random.seed(272) data_size = 100 x = np.random.uniform(low=1.0, high=10.0, size=data_size) y = x * 20 + 10 + np.random.normal(loc=0.0, scale=10.0, size=data_size) # plt.scatter(x, y, marker='.') # plt.show() # train / test split shuffled_index = np.random.permutation(data_size) x = x[shuffled_index] y = y[shuffled_index] split_index = int(data_size * 0.7) x_train = x[:split_index] y_train = y[:split_index] x_test = x[split_index:] y_test = y[split_index:] # visualize data # plt.scatter(x_train, y_train, marker='.') # plt.show() # plt.scatter(x_test, y_test, marker='.') # plt.show() # train the liner regression model regr = LinerRegression(learning_rate=0.01, max_iter=10, seed=314) regr.fit(x_train, y_train) print('cost: {:.3}'.format(regr.loss())) print('w: {:.3}'.format(regr.w)) print('b: {:.3}'.format(regr.b)) show_data(x, y, regr.w, regr.b) # plot the evolution of cost plt.scatter(np.arange(len(regr.loss_arr)), regr.loss_arr, marker='o', c='green') plt.show()
5.2 sklearn实现

# -*-coding:utf-8 -*- import numpy as np from bs4 import BeautifulSoup import random def scrapePage(retX, retY, inFile, yr, numPce, origPrc): """ 函数说明:从页面读取数据,生成retX和retY列表 Parameters: retX - 数据X retY - 数据Y inFile - HTML文件 yr - 年份 numPce - 乐高部件数目 origPrc - 原价 Returns: 无 """ # 打开并读取HTML文件 with open(inFile, encoding='utf-8') as f: html = f.read() soup = BeautifulSoup(html) i = 1 # 根据HTML页面结构进行解析 currentRow = soup.find_all('table', r = "%d" % i) while(len(currentRow) != 0): currentRow = soup.find_all('table', r = "%d" % i) title = currentRow[0].find_all('a')[1].text lwrTitle = title.lower() # 查找是否有全新标签 if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1): newFlag = 1.0 else: newFlag = 0.0 # 查找是否已经标志出售,我们只收集已出售的数据 soldUnicde = currentRow[0].find_all('td')[3].find_all('span') if len(soldUnicde) == 0: print("商品 #%d 没有出售" % i) else: # 解析页面获取当前价格 soldPrice = currentRow[0].find_all('td')[4] priceStr = soldPrice.text priceStr = priceStr.replace('$','') priceStr = priceStr.replace(',','') if len(soldPrice) > 1: priceStr = priceStr.replace('Free shipping', '') sellingPrice = float(priceStr) # 去掉不完整的套装价格 if sellingPrice > origPrc * 0.5: print("%d %d %d %f %f" % (yr, numPce, newFlag, origPrc, sellingPrice)) retX.append([yr, numPce, newFlag, origPrc]) retY.append(sellingPrice) i += 1 currentRow = soup.find_all('table', r = "%d" % i) def ridgeRegres(xMat, yMat, lam = 0.2): """ 函数说明:岭回归 Parameters: xMat - x数据集 yMat - y数据集 lam - 缩减系数 Returns: ws - 回归系数 """ xTx = xMat.T * xMat denom = xTx + np.eye(np.shape(xMat)[1]) * lam if np.linalg.det(denom) == 0.0: print("矩阵为奇异矩阵,不能求逆") return ws = denom.I * (xMat.T * yMat) return ws def setDataCollect(retX, retY): """ 函数说明:依次读取六种乐高套装的数据,并生成数据矩阵 Parameters: 无 Returns: 无 """ scrapePage(retX, retY, './lego/lego8288.html', 2006, 800, 49.99) #2006年的乐高8288,部件数目800,原价49.99 scrapePage(retX, retY, './lego/lego10030.html', 2002, 3096, 269.99) #2002年的乐高10030,部件数目3096,原价269.99 scrapePage(retX, retY, './lego/lego10179.html', 2007, 5195, 499.99) #2007年的乐高10179,部件数目5195,原价499.99 scrapePage(retX, retY, './lego/lego10181.html', 2007, 3428, 199.99) #2007年的乐高10181,部件数目3428,原价199.99 scrapePage(retX, retY, './lego/lego10189.html', 2008, 5922, 299.99) #2008年的乐高10189,部件数目5922,原价299.99 scrapePage(retX, retY, './lego/lego10196.html', 2009, 3263, 249.99) #2009年的乐高10196,部件数目3263,原价249.99 def regularize(xMat, yMat): """ 函数说明:数据标准化 Parameters: xMat - x数据集 yMat - y数据集 Returns: inxMat - 标准化后的x数据集 inyMat - 标准化后的y数据集 """ inxMat = xMat.copy() #数据拷贝 inyMat = yMat.copy() yMean = np.mean(yMat, 0) #行与行操作,求均值 inyMat = yMat - yMean #数据减去均值 inMeans = np.mean(inxMat, 0) #行与行操作,求均值 inVar = np.var(inxMat, 0) #行与行操作,求方差 # print(inxMat) print(inMeans) # print(inVar) inxMat = (inxMat - inMeans) / inVar #数据减去均值除以方差实现标准化 return inxMat, inyMat def rssError(yArr,yHatArr): """ 函数说明:计算平方误差 Parameters: yArr - 预测值 yHatArr - 真实值 Returns: """ return ((yArr-yHatArr)**2).sum() def standRegres(xArr,yArr): """ 函数说明:计算回归系数w Parameters: xArr - x数据集 yArr - y数据集 Returns: ws - 回归系数 """ xMat = np.mat(xArr); yMat = np.mat(yArr).T xTx = xMat.T * xMat #根据文中推导的公示计算回归系数 if np.linalg.det(xTx) == 0.0: print("矩阵为奇异矩阵,不能求逆") return ws = xTx.I * (xMat.T*yMat) return ws def crossValidation(xArr, yArr, numVal = 10): """ 函数说明:交叉验证岭回归 Parameters: xArr - x数据集 yArr - y数据集 numVal - 交叉验证次数 Returns: wMat - 回归系数矩阵 """ m = len(yArr) #统计样本个数 indexList = list(range(m)) #生成索引值列表 errorMat = np.zeros((numVal,30)) #create error mat 30columns numVal rows for i in range(numVal): #交叉验证numVal次 trainX = []; trainY = [] #训练集 testX = []; testY = [] #测试集 random.shuffle(indexList) #打乱次序 for j in range(m): #划分数据集:90%训练集,10%测试集 if j < m * 0.9: trainX.append(xArr[indexList[j]]) trainY.append(yArr[indexList[j]]) else: testX.append(xArr[indexList[j]]) testY.append(yArr[indexList[j]]) wMat = ridgeTest(trainX, trainY) #获得30个不同lambda下的岭回归系数 for k in range(30): #遍历所有的岭回归系数 matTestX = np.mat(testX); matTrainX = np.mat(trainX) #测试集 meanTrain = np.mean(matTrainX,0) #测试集均值 varTrain = np.var(matTrainX,0) #测试集方差 matTestX = (matTestX - meanTrain) / varTrain #测试集标准化 yEst = matTestX * np.mat(wMat[k,:]).T + np.mean(trainY) #根据ws预测y值 errorMat[i, k] = rssError(yEst.T.A, np.array(testY)) #统计误差 meanErrors = np.mean(errorMat,0) #计算每次交叉验证的平均误差 minMean = float(min(meanErrors)) #找到最小误差 bestWeights = wMat[np.nonzero(meanErrors == minMean)] #找到最佳回归系数 xMat = np.mat(xArr); yMat = np.mat(yArr).T meanX = np.mean(xMat,0); varX = np.var(xMat,0) unReg = bestWeights / varX #数据经过标准化,因此需要还原 print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % ((-1 * np.sum(np.multiply(meanX,unReg)) + np.mean(yMat)), unReg[0,0], unReg[0,1], unReg[0,2], unReg[0,3])) def ridgeTest(xArr, yArr): """ 函数说明:岭回归测试 Parameters: xMat - x数据集 yMat - y数据集 Returns: wMat - 回归系数矩阵 """ xMat = np.mat(xArr); yMat = np.mat(yArr).T #数据标准化 yMean = np.mean(yMat, axis = 0) #行与行操作,求均值 yMat = yMat - yMean #数据减去均值 xMeans = np.mean(xMat, axis = 0) #行与行操作,求均值 xVar = np.var(xMat, axis = 0) #行与行操作,求方差 xMat = (xMat - xMeans) / xVar #数据减去均值除以方差实现标准化 numTestPts = 30 #30个不同的lambda测试 wMat = np.zeros((numTestPts, np.shape(xMat)[1])) #初始回归系数矩阵 for i in range(numTestPts): #改变lambda计算回归系数 ws = ridgeRegres(xMat, yMat, np.exp(i - 10)) #lambda以e的指数变化,最初是一个非常小的数, wMat[i, :] = ws.T #计算回归系数矩阵 return wMat def useStandRegres(): """ 函数说明:使用简单的线性回归 Parameters: 无 Returns: 无 """ lgX = [] lgY = [] setDataCollect(lgX, lgY) data_num, features_num = np.shape(lgX) lgX1 = np.mat(np.ones((data_num, features_num + 1))) lgX1[:, 1:5] = np.mat(lgX) ws = standRegres(lgX1, lgY) print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % (ws[0],ws[1],ws[2],ws[3],ws[4])) def usesklearn(): """ 函数说明:使用sklearn Parameters: 无 Returns: 无 """ from sklearn import linear_model reg = linear_model.Ridge(alpha = .5) lgX = [] lgY = [] setDataCollect(lgX, lgY) reg.fit(lgX, lgY) print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % (reg.intercept_, reg.coef_[0], reg.coef_[1], reg.coef_[2], reg.coef_[3])) if __name__ == '__main__': usesklearn()
