function [ Xk ] = DFT( xn,N ) %定于DFT算法 xxn=zeros(1,N);%构造1*N的零矩阵 xxn(1:length(xn))=xn; %将形参赋值进来 Xk=ones(1,N);%构造1*N的全1矩阵 Wn=exp(-1i*2*pi/N);% wn=ones(N,N);%构造N*N的全1矩阵 for k=0:1:N-1 %DFT公式 for n=0:1:N-1 wn(k+1,n+1)=Wn^(k*n); end end Xk=(wn*xxn')';%矩阵转置相乘 end
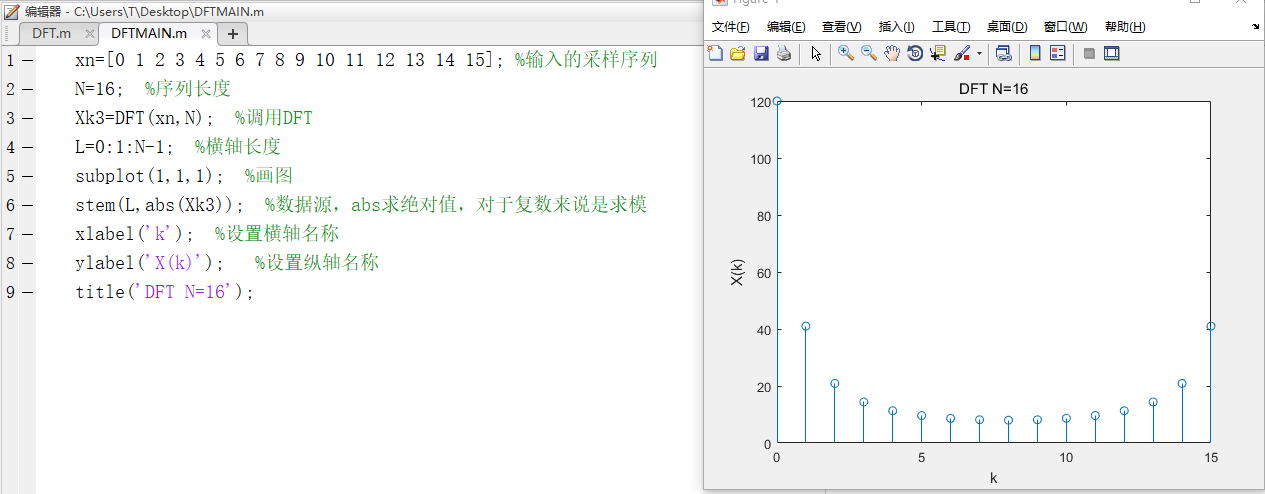
xn=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]; %输入的采样序列 N=16; %序列长度 Xk3=DFT(xn,N); %调用DFT L=0:1:N-1; %横轴长度 subplot(1,1,1); %画图 stem(L,abs(Xk3)); %数据源,abs求绝对值,对于复数来说是求模 xlabel('k'); %设置横轴名称 ylabel('X(k)'); %设置纵轴名称 title('DFT N=16');
实验结果: