题目描述
给你一个有 (n) 个点的森林,点有黑白两种颜色,初始时所有点都是白色,森林的每条边有边权,初始时这个森林有 (m) 条边。
对这个森林进行 (k) 次操作,操作有三种:
L u v w:添加一条连接 (u) 和 (v),长度为 (w) 的边。C u v:删除连接 (u) 和 (v) 的边(保证存在)。F u:反转点 (u) 的颜色(黑变白,白变黑)。Q u:询问所有与 (u) 相连的黑点到 (u) 的距离之和。(相连指的是在同一连通块中)
输入格式
第一行三个非负整数,分别表示 (n,m,k)。
以下 (m) 行,每行三个整数 (u,v,w),表示初始时有一条边连接 (u) 和 (v),长度为 (w)。
以下 (k) 行,每行描述一个操作,格式如上所述。
输出格式
对于每个 Q 操作,单独一行输出一个整数表示答案。
保证任何时候这个图都是一个森林。
题解
LCT维护子树信息
假设现在需要用LCT维护原树中一个子树的 (siz)
为了方便查询,一般会把原树中一条重链的顶端 (x) 的子树信息存储在((x) 在LCT中所在的二叉树的根)的位置
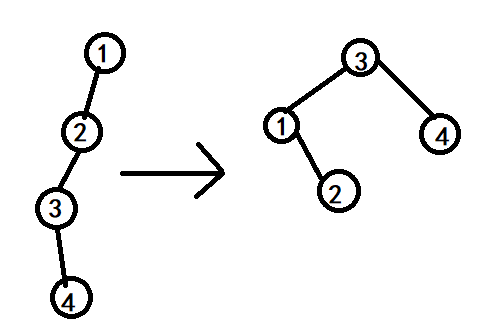
如上图,原树中的 (siz[1]) 实际上存在LCT中的 (siz[3]) 里,而 (siz[1]) 里存的其实是 (1) 和 (2) 的权值和
但是一个点子树的 (siz) 不仅包含自己所在的那条重链啊 如何维护轻子树的大小?
很简单,我们记 (lsiz[x]) 表示LCT中 (x) 的所有轻子树的 (siz) 之和,这样 (siz[x]) 就等于 (siz[lson]+siz[rson]+lsiz[x]+1)
如何维护 (lsiz) 呢?首先,在link(x,y)操作时 (y) 会变成 (x) 的一个新的轻儿子,所以 (lsiz[x]) 要加上 (siz[y])
其次,access时经过的点的重儿子变成了轻儿子,而某个轻儿子变成了重儿子,要注意更新 (lsiz)
总之记住轻儿子发生变化的时候记得更新 (lsiz) 即可
但是实际应用中我们肯定不会用LCT去维护子树 (siz) 这种这么简单的东西的(好像还真有,而且不少),所以来看看这道题
对于询问操作,其实我们可以通过LCT来做一个makeroot(u)的操作,这样每次询问就变成了询问所有黑点到根的距离之和了
对于每条边 (u,v),新建一个点 (w),把 (w) 的点权设为边权,把 (u,v) 的点权设为 (0),然后在LCT中连 (u,w) 和 (w,v),这样询问路径长度就变成询问路径上的点权和了

对于点 (x) 如何统计答案?
这里是一张LCT的部分图,图中的箭头表示某一个点走到根应该沿什么方向走
由于LCT中左子树的点在原树中深度较小,所以应该向左走
我们设 (sum[x]) 表示LCT中 (x) 子树的点权和,(siz[x]) 表示有多少个黑点,(lsiz[x]) 表示 (x) 的所有轻子树中共有多少个黑点
不难发现,如果图中所有点想要从 (x) 开始走到 (x) 所在重链的顶端,那么需要走过的路径长度是 (sum[lson]+val[x])
有多少个点要走过去呢?(lsiz[x]+siz[rson]) 个,如果 (x) 也是黑点就还要额外+1
所以这里 (x) 的答案就是 ((sum[lson]+val[x])*(lsiz[x]+siz[rson]+color[x]))
累加答案也可以用类似的方法 即(ans[x]=ans[lson]+ans[rson]+lightans[x]);(lightans[x]) 就是轻子树的答案之和
然后是一些细节:
进行access时,某个重儿子变成了轻儿子,而轻儿子变成了重儿子,所以要记得更新 (lsiz[x]) 之类的东西
注意,执行makeroot操作时翻转了整棵LCT,所以我们不仅要记录从右子树向左子树走的答案,还要记录从左到右的答案,这样才能 (O(1)) 翻转
时间复杂度 (O(nlog n))
代码还算较为好写
#include <bits/stdc++.h>
#define N 1000005
using namespace std;
typedef long long ll;
template<typename T>
inline void read(T &num) {
T x = 0, f = 1; char cch = getchar();
for (; cch > '9' || cch < '0'; cch = getchar()) if (cch == '-') f = -1;
for (; cch <= '9' && cch >= '0'; cch = getchar()) x = (x << 3) + (x << 1) + (cch ^ '0');
num = x * f;
}
template<typename T>
inline void write(T num) {
if (num < 0) putchar('-'), num = -num;
if (num > 9) write(num / 10);
putchar(num % 10 + '0');
}
int n, tot, m, q, ch[N][2], fa[N];
ll siz[N], lsiz[N], tp[N], sum[N], val[N], lans[N], rans[N], light[N], tag[N];
inline void pushup(int x) {
siz[x] = lsiz[x] + siz[ch[x][0]] + siz[ch[x][1]] + tp[x];
sum[x] = sum[ch[x][0]] + sum[ch[x][1]] + val[x];
lans[x] = lans[ch[x][0]] + lans[ch[x][1]] + light[x];
lans[x] += (sum[ch[x][0]] + val[x]) * (lsiz[x] + siz[ch[x][1]] + tp[x]);
rans[x] = rans[ch[x][0]] + rans[ch[x][1]] + light[x];
rans[x] += (sum[ch[x][1]] + val[x]) * (lsiz[x] + siz[ch[x][0]] + tp[x]);
}
inline void rev(int x) {
swap(ch[x][0], ch[x][1]);
swap(lans[x], rans[x]);
tag[x] ^= 1;
}
inline bool isroot(int x) { return ch[fa[x]][0] != x && ch[fa[x]][1] != x; }
inline void pushdown(int x) {
if (!tag[x]) return;
if (ch[x][1]) rev(ch[x][1]);
if (ch[x][0]) rev(ch[x][0]);
tag[x] = 0;
}
inline void rotate(int x) {
int y = fa[x], z = fa[y], k = (ch[y][1] == x);
if (!isroot(y)) ch[z][ch[z][1]==y] = x;
fa[x] = z;
ch[y][k] = ch[x][k^1]; fa[ch[x][k^1]] = y;
ch[x][k^1] = y; fa[y] = x;
pushup(y); pushup(x);
}
int stk[N], top;
inline void splay(int x) {
stk[top=1] = x;
for (int i = x; !isroot(i); i = fa[i]) stk[++top] = fa[i];
while (top) pushdown(stk[top--]);
while (!isroot(x)) {
int y = fa[x], z = fa[y];
if (!isroot(y)) {
((ch[y][1] == z) ^ (ch[z][1] == y)) ? rotate(x) : rotate(y);
}
rotate(x);
}
}
inline void access(int x) {
for (int i = 0; x; i = x, x = fa[x]) {
splay(x);
lsiz[x] -= (siz[i] - siz[ch[x][1]]);
light[x] -= (lans[i] - lans[ch[x][1]]);
ch[x][1] = i; pushup(x);
}
}
inline void makeroot(int x) {
access(x); splay(x); rev(x);
}
inline void link(int x, int y) {
makeroot(x); makeroot(y);
fa[x] = y;
lsiz[y] += siz[x];
light[y] += lans[x];
pushup(y);
}
inline void cut(int x, int y) {
makeroot(x); access(y); splay(y);
ch[y][0] = fa[x] = 0;
pushup(y);
}
map<pair<int, int> , int> mp;
int main() {
read(n); read(m); read(q);
tot = n;
for (int i = 1, u, v; i <= m; i++) {
read(u); read(v); read(val[++tot]);
link(u, tot); link(v, tot);
mp[make_pair(u, v)] = mp[make_pair(v, u)] = tot;
}
char s[5];
for (int i = 1, x, y; i <= q; i++) {
scanf("%s", s);
if (s[0] == 'L') {
read(x); read(y); read(val[++tot]);
link(x, tot); link(y, tot);
mp[make_pair(x, y)] = mp[make_pair(y, x)] = tot;
} else if (s[0] == 'C') {
read(x); read(y);
int z = mp[make_pair(x, y)];
mp[make_pair(x, y)] = mp[make_pair(y, x)] = 0;
cut(x, z); cut(y, z);
} else if (s[0] == 'F') {
read(x);
makeroot(x);
tp[x] ^= 1;
pushup(x);
} else {
read(x);
makeroot(x);
write(lans[x]);
puts("");
}
}
return 0;
}