数论模板(1) 质数判断、线性筛、朴素欧拉函数线性筛

1.素数的判断

从去年退役之后，本人重回竞赛界，开始新的人生，只是忘记的东西太多，一点点地复习吧
先来说质数的判断
首先，一个数是质数的充分必要条件是，除了1和本身没有其他因子，（顺便说一下1也不是素数，其实1被认为既不是素数也不是合数）。因此最最朴素的算法是枚举除了1和它本身之间的所有数，判断是否能整除。

int isprime(int n)
{	
	if(n==1)return 0;
	for(int i = 2; i < n; i ++)
	{
		if(n%i==0)return 0;
	}
	return 1;
}

显然，时间复杂度为O(n)
我们仔细观察，其实没有必要枚举到n,枚举到sqrt(n)（表示n的平方根）即可

int isprime(int n)
{
	if(n==1)return 0;
	for(int i = 2;i*i<=n; i++)//i*i<=n比i<=sqrt(n)更好，因为浮点运算比整数运算慢
	{
		if(n%i==0)return 0;
	}
	return 1;
}

时间复杂度优化至O(sqrt(n))
那么，有没有更快一点的算法呢？
有的…
如果在判断之前完成预处理，将所求范围内的所有质数存在一个数组中，枚举所有质数进行判断即可

int isprime(int n)
{
	if(n==1)return 0;
	for(int i = 1; prime[i]*prime[i]<= n; i++)
	{
		if(n%prime[i]==0)return 0;
	}
	return 1;
}

时间复杂度低于O(sqrt(n))（玄学）
那么问题来了，质数表如何求出呢？

2.线性筛质数表

线性筛是一种常用的质数表处理方式。
预处理质数表最容易想到的方式是枚举所有范围内的数，再用上面的方法判断是否为质数，
时间复杂度最少为O(sqrt(n)*n)
这太大了…
于是乎有了线性筛。
为了明白线性筛是怎么来的
我们先来看看最简单的筛法
从小到大枚举1到n的每一个数，
并用这个数筛掉所有所有它的倍数
比如枚举到2，就筛掉4，6，8，10，12…
并给这些数打上不是质数的标记
下面是代码

#define N 100000
char notprime[N];
int prime[N],tot;
int init()
{
	notprime[1]=1;
	for(int i = 2; i <= n; i ++)
	{
		if(!notprime[i])
		{
			prime[++tot]=i;
		}
		int j = 2;
		while(j*i<=n)
		{
			notprime[i*j]=1;	
			j++;
		}
	}
}

由调和级数可知，时间复杂度约为O(nlogn)
但是我们的目标是线性！！！
所以我们只需要枚举已经求出的素数表用于筛就可以了
另外，如果被枚举的素数是当前I的因子，同样可以跳过
因为已经被筛过一遍了
下面给出代码

#define N 100000
char notprime[N];
int prime[N],tot,n;
void init()
{
   	notprime[1]=1;
   	for(int i = 2; i <= n; i ++)
	{
 		if(!notprime[i])
 		{
 		 prime[++tot]=i;
 		}
   		for(int j = 1; j <= tot&&prime[j]*i<=n; j ++)
   		{
   			notprime[prime[j]*i]=1;
   			if(i%prime[j]==0)break;
   		}
	}
}

至此完成线性时间复杂度的算法
接下来，我们来学习欧拉函数！！！！

3.欧拉的邪恶函数

什么是欧拉函数？
欧拉函数是一种重要的数论函数，用希腊字母φ表示。讨论的是对于自然数n，小于n且与n互质的数的个数。
至于什么是互质，用gcd(a,b)表示a,b两数的最大公约数，gcd(a,b)=1则表示两数互质
（当然在欧拉函数中是不包括1的）
欧拉函数的朴素求法：

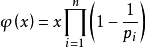
其中pi表示x的质因子
由此得出朴素欧拉函数的求法

int phi(int x)
{
	int ans = x;
	for(int i = 2; i*i <= x; i++)
	if(x%i==0)
	{
		ans = ans/i*(i-1);
		while(x%i==0)
		{
			x/=i;
		}
	}
	if(x>1)ans=ans/x*(x-1);
	return ans;
}

时间复杂度o(sqrt(n))

欧拉函数有很多鬼畜的特点
当p为质数时，φ§=p-1(显然 ）
欧拉函数是不完全积性函数
在gcd(m,n)=1时，φ(mn)=φ(m)φ(n)
特别地，在p为质数时，若gcd(m,p)=1,φ(mp)=φ(m)(p-1)
在p为质数时，若gcd(m,p)=p,φ(mp)=p*φ(m)
利用这些性质，我们可以在线性筛素数的同时完成线性筛欧拉函数

#define N 100006
char notprime[N];
int phi[N],prime[N],tot,n;
void init()
{
	notprime[1]=1;
	phi[1]=1;
	for(int i = 2; i <= n;i++)
	{
		if(!notprime[i])
		{
			phi[i]=i-1;
			prime[++tot]=i;
		}
		for(int j = 1; j <= tot && prime[j]*i<= n; j++)
		{
			notprime[prime[j]*i]=1;
			if(i%prime[j]==0)
			{
				phi[prime[j]*i]=prime[j]*phi[i];
				break;
			}
			else phi[prime[j]*i]=phi[i]*(prime[j]-1);
		}
	}
}

至此我们以O(n)复杂度完成了预处理了欧拉函数的值
现在我们来说说欧拉函数可以做什么

4.例题

洛谷P2158 仪仗队
题目描述
作为体育委员，C君负责这次运动会仪仗队的训练。仪仗队是由学生组成的N * N的方阵，为了保证队伍在行进中整齐划一，C君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐(如下图)。 现在，C君希望你告诉他队伍整齐时能看到的学生人数。

输入输出格式
输入格式：

共一个数N
输出格式：

共一个数，即C君应看到的学生人数。
链接：https://www.luogu.org/problemnew/show/P2158
经过分析，每多出一排，所增加的视线数目为φ(n)*2
因此我们套用模板求出他们的和就可以了
注意n=1时特判

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <queue>
using namespace std;
#define N 40005
bool notprime[N];
int prime[N],phi[N],tot,n;
void init()
{
    notprime[1]=1;
    phi[1]=1;
    for(int i = 2; i <= n; i ++)
    {
        if(!notprime[i])
        {
            prime[++tot]=i;phi[i]=i-1;
        }
        for(int j = 1;j<=tot&&prime[j]*i<=n;j++)
        {
            notprime[prime[j]*i]=1;
            if(i%prime[j]==0)
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }       
    }
}
int main()
{
    scanf("%d",&n);
    init();
    long long ans = 1;
    for(int i = 1; i <= n; i ++)
    {
        ans += phi[i-1]+phi[i-1];
    }
    if(n==1)ans--;
    printf("%lld",ans);
}