题目描述
对于一个长度为n的数列p,数列中任意两个数互质。准备一个无限长的储存器。然后从p1开始,把储存器中p1倍数位置都赋值为p1,把储存器中p2倍数位置都赋值为p2,把储存器中p3倍数位置都赋值为p3。。。把储存器中pn倍数位置都赋值为pn。最后求每个pi在储存器中出现的比例,用分数表示。
输入
n n个两两互质的数。
输出
输出n个分数
1<=n<=1000,1<=pi<=10^9
样例输入
3
2
3
5
样例输出
4/15 4/15 1/5
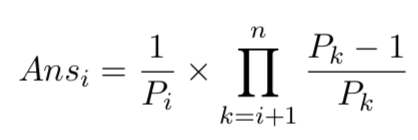
思路:如果从前往后做,之前统计过的会被之后的操作覆盖,所以我们从后往前统计.我们可以导出上面的式子(p为题目中输入的数)~但是,这道题需要输出最简分数,long long显然无法达到题目的要求(爆炸),所以我们需要写高精度.公式中第二部分可以用两个变量tmpa(分子),tmpb(分母)存乘积,边存边约分.
注意:若遇到1需要特判,因为1会占所有剩余的空隙,此时我们break掉并把后边的答案赋成0/1即可.
1 #include <cstdio> 2 #define N 1010 3 #define M 1000000000 4 using namespace std; 5 int n,D; 6 struct gaojingdu{ 7 long long a[2010],clong; 8 void jinwei(){ 9 for(int i=1;i<clong;i++){ 10 a[i+1]+=a[i]/M; 11 a[i]%=M; 12 } 13 while(a[clong]>=M){ 14 clong++; 15 a[clong]=a[clong-1]/M; 16 a[clong-1]%=M; 17 } 18 while(a[clong]==0&&clong>1) clong--; 19 } 20 void print(){ 21 int i; 22 printf("%lld",a[clong]); 23 for(i=clong-1;i>=1;i--) 24 printf("%09lld",a[i]); 25 } 26 }; 27 int a[N]; 28 gaojingdu A[N],B[N]; 29 gaojingdu tmpa,tmpb,ret; 30 void initialize(gaojingdu &x,int y){ 31 x.clong=1; 32 x.a[1]=y; 33 } 34 int operator %(const gaojingdu &x,int y){ 35 long long ret=0; 36 for(int i=x.clong;i>=1;i--) 37 ret=(ret*M+x.a[i])%y; 38 return (int)ret; 39 } 40 gaojingdu operator *(const gaojingdu &x,int y){ 41 for(int i=1;i<=ret.clong;i++) 42 ret.a[i]=0; 43 ret.clong=x.clong; 44 for(int i=1;i<=x.clong;i++) 45 ret.a[i]=x.a[i]*y; 46 ret.jinwei(); 47 return ret; 48 } 49 gaojingdu operator /(const gaojingdu &x,int y){ 50 for(int i=1;i<=ret.clong;i++) 51 ret.a[i]=0; 52 long long tmp=0; 53 ret.clong=x.clong; 54 for(int i=x.clong;i>=1;i--){ 55 tmp=tmp*M+x.a[i]; 56 ret.a[i]=tmp/y; 57 tmp%=y; 58 } 59 ret.jinwei(); 60 return ret; 61 } 62 int gcd(int a,int b){ 63 if(a==0) 64 return b; 65 return gcd(b%a,a); 66 } 67 int gcd(int a,const gaojingdu &b){ 68 int tmp=b%a; 69 return gcd(a,tmp); 70 } 71 int main(){ 72 scanf("%d",&n); 73 int u,d,X,Y; 74 for(int i=1;i<=n;i++) 75 scanf("%d",&a[i]); 76 initialize(A[n],1);//A:答案分母 77 initialize(B[n],a[n]);//B:答案分子 78 initialize(tmpa,a[n]-1);//tmpa:后缀积的分子 79 initialize(tmpb,a[n]);//tmpb:后缀积的分母 80 for(int i=n-1;i>=1;i--){ 81 u=a[i]-1,d=a[i];//将要把u,d乘到tmp中 82 if(u!=0){ 83 X=gcd(u,tmpb);//分别对两组分子分母进行约分 84 Y=gcd(d,tmpa); 85 u/=X,d/=Y;//现在u与tmpb互质,d与tmpa互质 86 A[i]=tmpa/Y;//约分后代入 87 B[i]=tmpb*d; 88 tmpa=A[i]*u;//A[i]分母仍然是tmpa 89 tmpb=B[i]/X; 90 } 91 else{//遇到1时需要特判 92 D=i-1;//会把之前的覆盖 93 A[i]=tmpa;//*1不变 94 B[i]=tmpb; 95 break; 96 } 97 } 98 for(int i=1;i<=D;i++) 99 printf("0/1 "); 100 for(int i=D+1;i<=n;i++){ 101 A[i].print(); 102 printf("/"); 103 B[i].print(); 104 printf(" "); 105 } 106 return 0; 107 }