原根、与原根的应用(更新中)

阶：设a，p是整数，a和p互素，那么：使

  

成立的最小正整数n叫做a模p的阶.

 

 

原根:设m是正整数，a是整数，若a mod m的阶等于φ(m)，则称a为模m的一个原根.（其中φ(m)表示m的欧拉函数）

假设一个数g是质数P的原根，那么的结果两两不同，且有 1<g<P，0<i<P，归根到底就是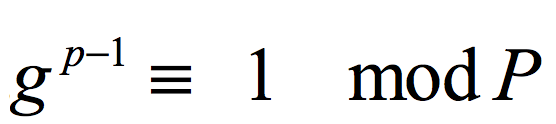当且仅当指数为P-1的时候成立.

 

有了这个上面性质,就可以容易的求出质数P的原根了.

Step1 将P-1进行质因数分解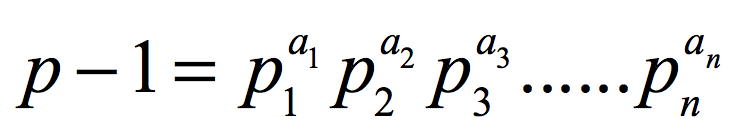

Step2 枚举i,并判断对于每个i是否都有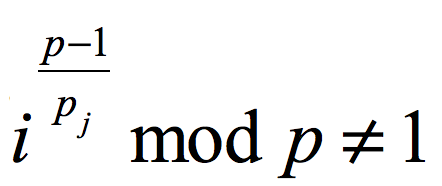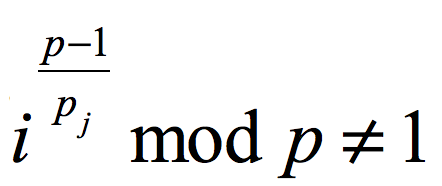(可以应用快速幂)

第一个符合条件的i就是P的最小原根

 

对于合数,只要将Step2中的p-1替换成φ(p)即可.

 

这里是代码

#include <cmath>
#include <cstdio>
#define ll long long
#define maxn 1000010
bool vis[maxn];
ll p,prime[maxn],cnt;
ll fp(ll x,ll a){
    ll ret=1;
    for(x%=p;a;a>>=1,x=x*x%p)
        if(a&1) ret=ret*x%p;
    return ret; 
}
void get_prime(int x){//筛出x以内的素数
    for(int i=2;i<=x;i++){
        if(!vis[i]) prime[++cnt]=i;
        for(int j=1;j<=cnt;j++){
            if(i*prime[j]>x) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}
bool check(ll x){//检查x是否是p的原根
    ll t=sqrt(x)+10;
    for(int i=1;prime[i]<=t;i++){
        if((p-1)%prime[i]==0&&fp(x,(p-1)/prime[i])%p==1)
            return 0;
    }
    return 1;
}
int main(){
    scanf("%lld",&p);
    get_prime(maxn);
    for(int i=1;i<=1000000;i++){
        if(check(i)){
            printf("%d
",i);
            return 0;
        }
    }
}