迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
迪杰斯特拉算法图解
以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。
初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
迪杰斯特拉算法的代码说明
以"邻接矩阵"为例对迪杰斯特拉算法进行说明,对于"邻接表"实现的图在后面会给出相应的源码。
1. 基本定义
// 邻接矩阵
typedef struct _graph
{
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph;
// 边的结构体
typedef struct _EdgeData
{
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
}EData;
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。
2. 迪杰斯特拉算法
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
} Graph,*PGraph;
typedef struct EdgeData
{
char start;
char end;
int weight;
} EData;
static int get_position(Graph g,char ch)
{
int i;
for(i=0; i<g.vexnum; i++)
if(g.vexs[i]==ch)
return i;
return -1;
}
Graph* create_graph()
{
char vexs[]= {'A','B','C','D','E','F','G'};
int matrix[][7]=
{
{0,12,INF,INF,INF,16,14},
{12,0,10,INF,INF,7,INF},
{INF,10,0,3,5,6,INF},
{INF,INF,3,0,4,INF,INF},
{INF,INF,5,4,0,INF,8},
{16,7,6,INF,2,0,9},
{14,INF,INF,INF,8,9,0}
};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int i,j;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(pG));
pG->vexnum=vlen;
for(i=0; i<pG->vexnum; i++)
pG->vexs[i]=vexs[i];
for(i=0; i<pG->vexnum; i++)
for(j=0; j<pG->vexnum; j++)
pG->matrix[i][j]=matrix[i][j];
for(i=0; i<pG->vexnum; i++)
{
for(j=0; j<pG->vexnum; j++)
{
if(i!=j&&pG->matrix[i][j]!=INF)
pG->edgnum++;
}
}
pG->edgnum/=2;
return pG;
}
void print_graph(Graph G)
{
int i,j;
printf("Matrix Graph:
");
for(i=0; i<G.vexnum; i++)
{
for(j=0; j<G.vexnum; j++)
printf("%10d ",G.matrix[i][j]);
printf("
");
}
}
EData* get_edges(Graph G)
{
EData *edges;
edges=(EData*)malloc(G.edgnum*sizeof(EData));
int i,j;
int index=0;
for(i=0; i<G.vexnum; i++)
{
for(j=i+1; j<G.vexnum; j++)
{
if(G.matrix[i][j]!=INF)
{
edges[index].start=G.vexs[i];
edges[index].end=G.vexs[j];
edges[index].weight=G.matrix[i][j];
index++;
}
}
}
return edges;
}
void dijkstra(Graph G,int vs,int prev[],int dist[])
{
int i,j,k;
int min;
int tmp;
int flag[MAX];
for(i=0;i<G.vexnum;i++)
{
flag[i]=0;
prev[i]=vs;
dist[i]=G.matrix[vs][i];
}
flag[vs]=1;
dist[vs]=0;
for(i=1;i<G.vexnum;i++)
{
min=INF;
for(j=0;j<G.vexnum;j++)
{
if(flag[j]==0&&dist[j]<min)
{
min=dist[j];
k=j;
}
}
flag[k]=1;
for(j=0;j<G.vexnum;j++)
{
tmp=((G.matrix[k][j]==INF)?INF:(min+G.matrix[k][j]));
if(flag[j]==0&&tmp<dist[j])
{
dist[j]=tmp;
prev[j]=k;
}
}
}
printf("dijktra(%c):
",G.vexs[vs]);
for(i=0;i<G.vexnum;i++)
printf(" shortest (%c,%c)=%d
",G.vexs[vs],G.vexs[i],dist[i]);
}
int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
int prev[MAX];
int dist[MAX];
dijkstra(*pG,3,prev,dist);
int i;
for(i=0;i<pG->vexnum;i++)
printf("%c %c
",pG->vexs[prev[i]],pG->vexs[i]);
}
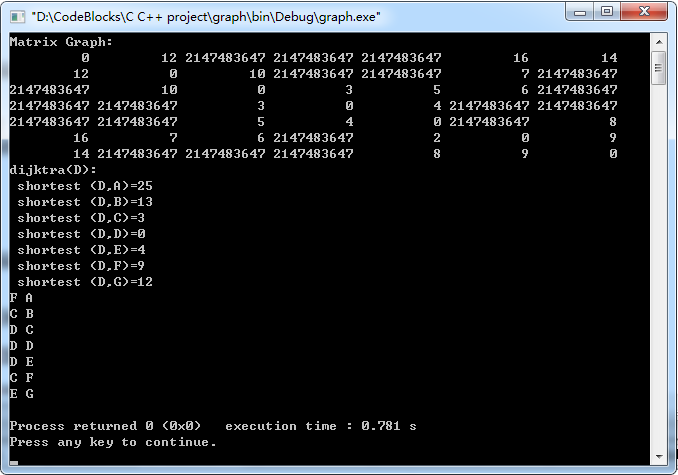
运行结果: