set 叫做集合
作用:
去重(去除重复)
举例——
>>> name_list = ['alben','nichole','lucy','andy','tom','alben']
>>> type(name_list)
<class 'list'>
>>> name_list
['alben', 'nichole', 'lucy', 'andy', 'tom', 'alben']
这个list中,有一个元素重复出现了2次‘alben’
通过set可以进行去重
>>> set1 = set(name_list)
>>> set1
{'andy', 'tom', 'lucy', 'nichole', 'alben'}
对set可以实施的操作:
1,‘add’ 追加元素
>>>set1.add('curry')
>>> set1
{'andy', 'lucy', 'tom', 'alben', 'curry', 'nichole'}
2,‘clear’ 清除所有元素
>>> set1.clear()
>>> set1
set()
3,‘difference’ 把set与列表进行对比,找出不同的
>>> name_list1 = ['alben','nichole','andy','lucy','tom','stephen']
>>> name_list2 = ['harden','tom','curry','thompson']
>>> set1 = set(name_list1)
>>> set1.difference(name_list2)
{'stephen', 'nichole', 'alben', 'andy', 'lucy'}
解释:
在这里有两个列表:name_list1,与name_list2,
通过set()把name_list1转换成了set,并且命名为set1
对set1进行difference(),与name_list2 进行对比,输出的结果是
{'stephen', 'nichole', 'alben', 'andy', 'lucy'}
其实就是把set1与name_list1进行对比,取出哪些set1中存在的,但是name_list2中没有的元素。
可以把difference的结果输出到表格或者另一个set
>>> name_list3 =[set1.difference(name_list2)] #如果这里不加【】的话,name_list3 就是一个‘set’
>>> type(name_list3)
<class 'list'>
>>> name_list3
[{'stephen', 'nichole', 'alben', 'andy', 'lucy'}]
4,difference_update 与difference的功能相同,都是寻找不同的元素,差别是difference_update直接更新原有set
>>> set1.difference_update(name_list2)
>>> set1
{'stephen', 'nichole', 'alben', 'andy', 'lucy'}
#效果显而易见#
5、remove 从set中删除一个元素
>>> set1
{'stephen', 'nichole', 'alben', 'andy', 'lucy'}
>>> set1.remove('andy')
>>> set1
{'stephen', 'nichole', 'alben', 'lucy'}
6,discard 从set中删除一个元素
>>> set1
{'stephen', 'nichole', 'alben', 'andy', 'lucy'}
>>> set1.discard('andy')
>>> set1
{'stephen', 'nichole', 'alben', 'lucy'}
remove()与discard()的区别:
remove()如果元素不不存在,报错
discard()如果元素不存在,不会报错
7,intersection 交集(初中数学集合知识)
>>> set1
{'stephen', 'tom', 'nichole', 'alben', 'andy', 'lucy'}
>>> name_list2
['harden', 'tom', 'curry', 'thompson']
>>> set3 = set1.intersection(name_list2)
>>> set3
{'tom'}
用图解释交集
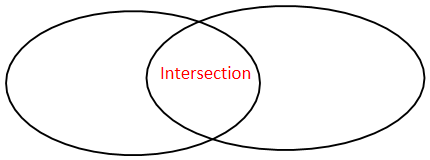
7,intersection_update(获取交集,在原来的set上进行升级,而不是输出到新的set)
8,isdisjoint 判断是否相交
如果相交 返回 False
反之,返回True
>>> s1
{1, 2, 3, 4, 5}
>>> num2
[6, 7, 8, 9, 10]
>>> num3
[1, 3, 5, 7, 9]
>>> s1.isdisjoint(num2)
True
>>> s1.isdisjoint(num3)
False
8、issubset 判断集合中的所有元素是否在给定的列表/集合中
举例:
>>> num1
[1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> num2
[1, 3, 5, 7, 9]
>>> num3
[0, 2, 4, 6, 8]
>>> s1=set(num2)
>>> s1
{1, 9, 3, 5, 7}
>>> s1.issubset(num1)
True
9,issuperset 判断当前集合是否全部包含给定的列表/集合
>>> s1
{1, 9, 3, 5, 7}
>>> s0
{1, 2, 3, 4, 5, 6, 7, 8, 9}
>>> s0.issuperset(s1) #s0完全包含s1# 所以返回True
True
>>> s1.issuperset(s0) #s1并不是完全包含s0# 所以返还False
False
10,symmetric_difference()
用法:
set1.symmetric_difference(set2)
图示:
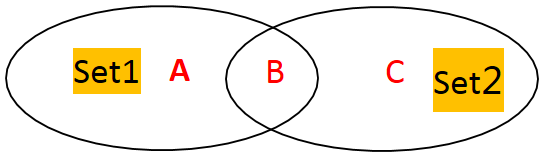
结果:
B删除,输出A+C
示例:
>>> num1=[1,2,3,4,5,6]
>>> num2=[2,4,6,8,10]
>>> s1 = set(num1)
>>> s1
{1, 2, 3, 4, 5, 6}
>>> s1.symmetric_difference(num2)
{1, 3, 5, 8, 10}
解释#在s1中有{1,2,3,4,5,6}
在list=num2中有[2,4,6,8,10]
解答:
交集部分:
[2 4 6]
C 独有部分 [8,10]
最后 {1,2,3,4,5,6}-[2,4,6]+[8,10]=[1,3,5,8,10]
11,symmetric_difference_update()
同理symmetric_difference,只是只是在原set上更新
12,union(合并)
>>> s1
{1, 2, 3, 4, 5, 6}
>>> s2
{8, 2, 10, 4, 6}
>>> s1.union(s2)
{1, 2, 3, 4, 5, 6, 8, 10}
13,update 添加多个元素