所谓凸包,就是给你一堆点,让你找一个最小的凸多边形(二维),使其包含所有点。这个凸多边形就是这些点的凸包。可以理解为是用橡皮筋把很多钉子围住的状态。
这些是凸包:
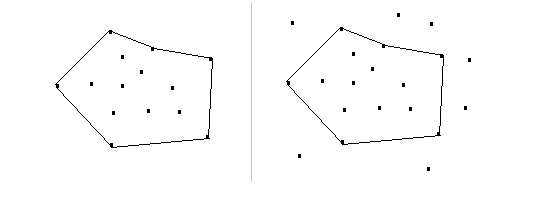
这些不是:
那么我们如何构造凸包呢?可以看出,如果我们按 (x) 排序的话,我甚至不想证明,最左和最右端点一定在凸包上。这样我们就可以把整个凸包分成上下两个”半凸包“来分别构造。
对于半凸包而言,其实是有一个很强的性质的,就是对于这半边凸包上的边而言,斜率的变化是单调的。在上凸包的边斜率单调减,在下凸包的边斜率单调增,并且这也很好用三角不等式证明。
那么我们准备逆用这个性质。 问题就转化为了:已知许多点的坐标,求出一条连接 (p_0) 到 (p_n) 的路径,使路径权值单调。其中每条边的权值就是这条边的斜率。
好的,果断使用单调栈。刚开始将 (p_0) 与 (p_n) 加入,每次向栈内投入一个元素 ((x_0,y_0)),求出与当前栈顶元素 ((x_1,y_1)) 和栈内下一位元素 ((x_2,y_2)) 的斜率并比较,若符合单调规则则加入,否则弹出栈顶元素,迭代 ((x_3,y_3)),重复上述操作直至回到初始点或满足条件。
对于比较斜率的算法,大佬们使用的都是向量叉积,把两条边看做向量用 (vec{a} , vec{b}) 表示,然后通过求叉积——((x_0-x_1,y_0-y_1)) 和 ((x_0-x_2,y_0-y_2)) 的叉积为 ((x_0-x_1)*(y_0-y_2)-(x_0-x_2)*(y_0-y_1))——与零的大小判断。但作为蒟蒻怎么可能会这些奇怪的东西!所以我找了一种稍微通俗那么一点点的方式来解释。
我们有两条边,一条斜率为 (k_1=frac{y_0-y_1}{x_0-x_1}),另一条斜率为 (k_2=frac{y_0-y_2}{x_0-x_2}) 。作差法可得
因为按 (x) 排序,所以 (x_0>x_1>x_2)。则 (k_2-k_1) 的符号与 ((y_0-y_2)(x_0-x_1)-(y_0-y_1)(x_0-x_2)) 符号相同。
这特么和叉积有什么区别?!
至此凸包构造完毕。