【数据结构之二叉树】

前言

我叫lvy，从校到参加工作，学习技术依赖已有两年多得时间，期间没有坚持过写点什么，感觉没有收获什么。有一句话说开始做一件事情任何时间都不晚，因此我开通了博客园，开始记录我的工作和生活。

现在从C语言开始我的第一篇博客，因为我的入门语言为C语言。之后会持续编写Java方面的见解。与大家共同成长。

【数据结构之二叉树】

二叉树是一个非常重要的树形结构，它的存储结构和运算都较为简单，而树也很容易转换成二叉树，本文主要探讨二叉树的遍历，一共分为前序、中序和后序三种遍历方式，使用递归进行遍历代码简介易懂。下面先介绍递归前序遍历及非递归方式的中序和后序遍历。

二叉树遍历的定义

1. 先序遍历。
   如果二叉树为空，则空操作；否则依次执行以下操作。

• 访问根结点
• 先序遍历根结点的左子树
• 先序遍历根结点的右子树

2. 中序遍历
   如果二叉树为空，则空操作；否则依次执行以下操作。

• 中序遍历根结点的左子树
• 访问根结点
• 中序遍历根结点的右子树

3. 后序遍历
   如果二叉树为空，则空操作；否则依次执行以下操作。

• 后序遍历根结点的左子树
• 后序遍历根结点的右子树
• 访问根节点

二叉树例图
与本文定义类型不符。

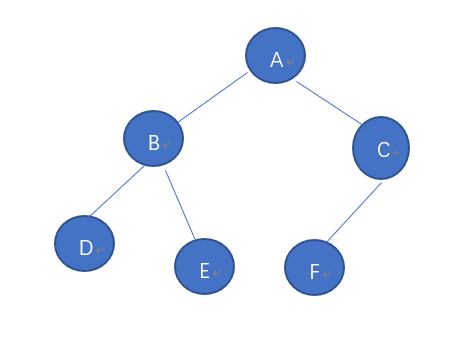
二叉树的类型描述

typedef struct BTNode
{
	int elem;
	struct BTNode *left,*right;
}*BinTree;

【先序遍历】

void PreOrder(BinTree root)
{
	if(root!=NULL)
	{
		printf("%4d",root->elem);  /*访问根结点*/
		PreOrder(root->left);      /*先序遍历根结点的左子树*/
		PreOrder(root->right);     /*先序遍历根结点的右子树*/
	}
}

中序遍历和后续递归遍历  
在此不做过多的介绍，那就开始上非递归遍历吧。

【非递归中序遍历】  
二叉树中序遍历的非递归算法的主要思想是令变量root为指向根节点的指针，从根结点开始遍历。显然，第一次遇到根结点并不进行访问，而是入栈，因为此时root所指根结点及其右子树尚未被访问，必须将root保存在栈中，以便在访问完左子树后，从栈中取出root，对其所指根结点及其右子树进行访问。在root进栈后，就中序遍历它的左子树，即把root的左孩子赋给root，沿左链走下去，直到左链为空，左子树遍历完毕，此时节点出站，把栈定元素赋给root，这是第二次遇到该节点，此时其左子树已经访问完毕，按照中序遍历的定义，访问根结点(打印该节点的信息)，随后中序遍历其右子树，即把root的右孩子赋给root,重复上述过程，直至root为空栈则结束。
其大致概括为：

1. 入栈后检测左边。出栈后检测右边。
2. 非递归中序遍历的特点是先进栈根节点，然后在判断有没有左节点
3. 如果有继续进栈，如果为空，出栈，出栈后判断有没有右节点
4. 如果有右节点进栈。然后以此类推。进栈的动作是连续的(只要有左节点就一直进栈),而出栈
   的动作只有一次。因为出栈后会判断有没有右节点，如果有且该节点不为空会重复上述过程，否继续出栈。

定义栈

#define MaxSize
typedef struct
{
	BinTree elem[MaxSize];
	int top;
}SeqStack;

中序遍历非递归实现算法描述：

void InOrder(BinTree root)
{
	SeqStack s;
	s.top=-1;
	do
	{
		while(root!=NULL)
		{
			s.top++;
			if(s.top>=MaxSize-1)
			{
				printf("栈已经满了!
");
				return ;
			}
			else
			{
				s.elem[s.top]=root;
				root=root->left;
			}
		}
		if(s.top!=-1)
		{
			root=s.elem[s.top];
			s.top--;
			printf("
%4d",root->elem);
			root=root->right;
		}
	}while((s.top!=-1)||(root!=NULL));
	
}

【非递归后续遍历】

1. 设置栈顶为-1，当根节点不为空时，进栈并设置该节点的访问次数为零，再次判断有没有左元素，如果有继续进栈。（左元素为空结束）
2. 出栈，退出之后判断栈是否为空，不为空时取出栈顶元素。判断是否有右孩子或者被访问的次数是否为零。
3. 如果没有右孩子且被访问次数为1时出栈。否则(也就是说有右孩子并且访问次数为零时)设置该节点的被访问次数为1.再把右孩子地址赋值给该节点。
4. 判断该节点是否为空。不为空时进栈并设置该节点的访问次数为零。访问左元素。依次循环（结合代码）

void PostOrder(BinTree root)
{
	SeqStack s;
	s.top=-1;
	while(root!=NULL)
	{
		s.top++;
		if(s.top==MaxSize-1)
		{
			printf("栈已经满了!
");
			printf("Error");
		}
		else
		{
			root->count=0;
			s.elem[s.top]=root;
			root=root->left;
		}
	}
	while(s.top!=-1)
	{
		root=s.elem[s.top];
		if(root->right==NULL||root->count==1)
		{
			printf("
%c",root->elem);
			s.top--;
		}
		else if(root->right!=NULL&&root->count!=1)
		{
			root->count=1;
			root=root->right;
			while(root!=NULL)
			{
				s.top++;
				s.elem[s.top]=root;
				root->count=0;
				root=root->left;
			}
		}
	}
}

前序遍历：A B D E C F
中序遍历：D B E A F C
后序遍历：D E B F C A