数据结构和算法概述
数据结构就是把数据元素按照一定的关系组织起来的集合,用来组织和存储数据
数据结构分为逻辑结构和物理结构两大类
逻辑结构分类
a.集合结构:集合结构中数据元素除了属于同一个集合外,他们之间没有任何其他的关系。
b.线性结构:线性结构中的数据元素之间存在一对一的关系。
c.树形结构:树形结构中的数据元素之间存在一对多的层次关系
d.图形结构:图形结构的数据元素是多对多的关系
物理结构分类
顺序存储结构:把数据元素放到地址连续的存储单元里面,其数据间的逻辑关系和物理关系是一致的 ,比如我们常用的数组就是顺序存储结构。
链式存储结构:数据元素存放在任意的存储单元里面,这组存储单元可以是连续的也可以是不连续的。此时,数据元素之间并不能反映元素间的逻辑关系,
因此在链式存储结构中引进了一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置。
算法
根据一定的条件,对一些数据进行计算,得到需要的结果。
在程序中,我们可以用不同的算法解决相同的问题,而不同的算法的成本也是不相同的。
总体上,一个优秀的算法追求以下两个目标:
1.花最少的时间完成需求;
2.占用最少的内存空间完成需求;
算法的复杂度分析
时间复杂度分析
时间复杂度分析实例

大O记法规则
推导大O阶的表示法有以下几个规则可以使用
- 用常数1取代运行时间中的所有加法常数;
- 在修改后的运行次数中,只保留高阶项;
- 如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
常见的大O阶
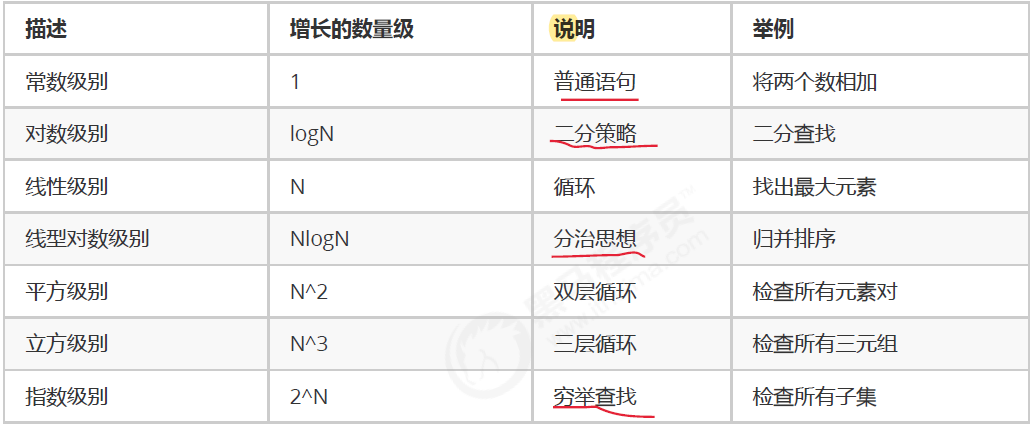
复杂程度从低到高依次为:O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)
我们提到的运行时间都指的是最坏情况下的运行时间.
空间复杂度分析

排序算法(笔试题)
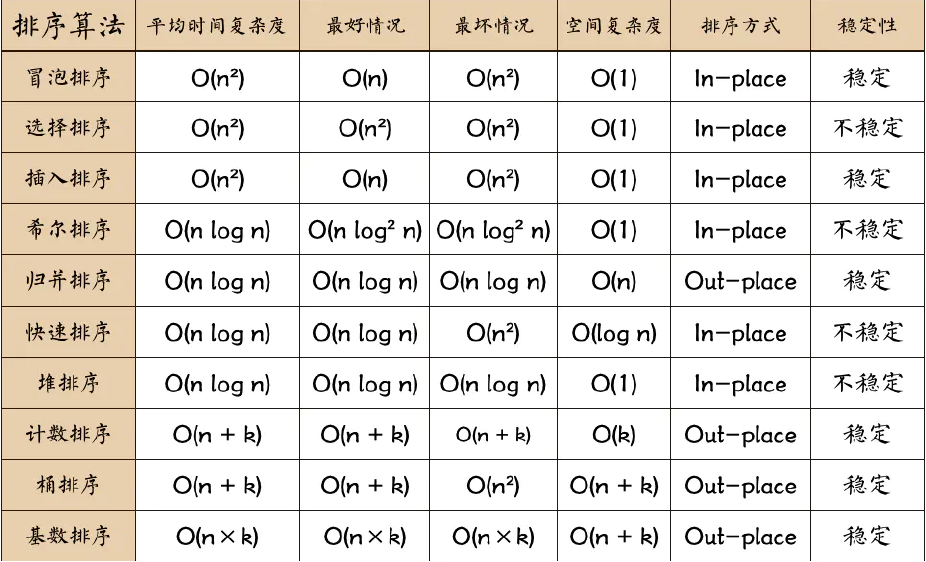
稳定:如果a原本在b前面且a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面且a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
手撕 冒泡排序
原理:由上至下,每行对相邻两个元素进行大小比较,若左边的大,则交换位置。
public class BubbleSort {
public static void main(String[] args) {
Integer[] aArray= {4,5,6,3,2,1};
bubbleSort(aArray);
System.out.println(Arrays.toString(aArray));
}
public static void bubbleSort(Comparable[] a){
for(int i=a.length-1;i>0;i--){
for(int j=0;j<i;j++){
if(Sort(a[j],a[j+1])){
exchange(a,j,j+1);
}
}
}
}
public static boolean Sort(Comparable lTemp, Comparable rTemp){
return lTemp.compareTo(rTemp)>0;
}
public static void exchange(Comparable[] a,int i,int j){
Comparable temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
手撕 快速排序
package simple;
import java.util.Arrays;
/**
* @Author hwj
* @Date 2020/8/14 9:41
* @Desc: 快速排序是对冒泡排序的一种改进。它的基本思想是:
* 一轮排序:
* 定义第一个数字为基准,右指针指向最右侧,左指针指向最左侧
* 先动右指针,当发现比基准小,记录右指针位置
* 再动左指针,发现比基准大,记录左指针位置
* 交换左右指针位置元素
* 再循环先右后左,直至左指针+1>右指针
* 交换基准元素与右指针
* 或者右指针-1=0,则数组不变
*
* 分隔:
* 通过一趟排序将要排序的数据分割成独立的两部分,
* 其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,
* 整个排序过程可以递归进行,以此达到整个数据变成有序序列。
**/
public class QuickSort {
public static void main(String[] args) {
Integer[] arr = {6, 1, 2, 7, 9, 3, 4, 5, 8};
sort(arr);
System.out.println(Arrays.toString(arr));
}
// 主排序方法入口
public static void sort(Comparable[] arr){
int lo=0;
int hi=arr.length-1;
sort(arr,lo,hi);
}
// 分段排序方法入口
public static void sort(Comparable[] arr,int lo,int hi){
// 当两个指针相遇,结束递归
if (hi<=lo){
return;
}
//对数组中,从lo到hi的元素进行切分
int partition = partition(arr, lo, hi);
//对左边分组中的元素进行排序
sort(arr,lo,partition-1);
//对右边分组中的元素进行排序
sort(arr,partition+1,hi);
}
// 数组切分
public static int partition(Comparable[] arr,int lo,int hi){
Comparable key=arr[lo];// 把最左边的元素当做基准值
int left=lo;// 定义一个左侧指针,初始指向最左边的元素
int right=hi+1;// 定义一个右侧指针,初始指向左右侧的元素下一个位置
//进行切分
while(true){
//先从右往左扫描,找到一个比基准值小的元素
while(less(key,arr[--right])){//循环停止,证明找到了一个比基准值小的元素
if (right==lo){
break;//已经扫描到最左边了,无需继续扫描
}
}
//再从左往右扫描,找一个比基准值大的元素
while(less(arr[++left],key)){//循环停止,证明找到了一个比基准值大的元素
if (left==hi){
break;//已经扫描到了最右边了,无需继续扫描
}
}
if (left>=right){
//扫描完了所有元素,结束循环
break;
}else{
//交换left和right索引处的元素
exch(arr,left,right);
}
}
//交换最后rigth索引处和基准值所在的索引处的值
exch(arr,lo,right);
return right; //right就是切分的界限
}
/*
数组元素i和j交换位置
*/
private static void exch(Comparable[] arr, int i, int j) {
Comparable t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
/*
比较v元素是否小于w元素
*/
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
}
-
代码实现
1)队列操作
-
package queue; import java.util.Scanner; public class QueueOp { public static void main(String[] args) { ArrayQueue queue = new ArrayQueue(3); char key = ' '; Scanner scanner = new Scanner(System.in); boolean loop = true; // 输出队列 while (loop) { System.out.println("s(show):显示队列"); System.out.println("e(exit):退出程序"); System.out.println("a(add):添加数据到队列"); System.out.println("g(get):从队列取出数据"); System.out.println("l(location):显示队列指定位置数据"); key = scanner.next().charAt(0); switch (key) { case 's': queue.ShowQueue(); break; case 'a': System.out.println("输出一个数"); int value = scanner.nextInt(); queue.addQueue(value); break; case 'g': try { int res = queue.outQueue(); System.out.printf("取出的数据是%d ", res); } catch (Exception e) { e.printStackTrace(); } break; case 'l': int appoint = scanner.nextInt(); queue.ShowAppoint(appoint); } } } } // 初始化 class ArrayQueue { /** * 变量声明: * 1 数组最大容量 * 2 队列头 * 3 队列尾 * 4 队列数组(一维) */ private int MaxSize; private int front; private int rear; private int[] queue; public ArrayQueue(int MaxSize) { // 对声明的变量进行初始化 this.MaxSize = MaxSize; front = -1; rear = -1; queue = new int[MaxSize]; } // 判断队列是否满 public boolean isFull() { return rear == MaxSize; } // 判断队列是否为空 public boolean isEmpty() { return front == rear; } // 加数据 public void addQueue(int n) { if (isFull()) { System.out.println("队列满,不能加入数据~"); return; } rear++; //让rear后移 queue[rear] = n; } // 取数据 public int outQueue() { if (isEmpty()) { throw new RuntimeException("队列空,不能取数据~"); } front++; //让front后移 return queue[front]; } // 显示队列所有数据 public void ShowQueue() { if (isEmpty()) { throw new RuntimeException("队列空,无数据~"); } int t = -1; t++; //让front后移 System.out.printf("queue [%d]=%d/t", t, queue[t]); } //显示队列指定位置数据 public void ShowAppoint(int appoint) { if (appoint <= -1 || appoint >= MaxSize) { throw new RuntimeException("队列空,无数据~"); } int t = -1; t++; //让front后移 System.out.printf("queue [%d]=%d ", t, queue[t]); } }
2)环形队列
关键点:
1)int[] arr 是定义一个整型数组当队列
2)maxSize是数组的最大容量
(这里规定,满队列时元素的个数是maxSize-1)
3)front指向队列的第一个元素,也就是说 array[front] 是队列的第一个元素
4)rear指向队列的最后一个元素,初值为0
5)队列满的条件:(rear + 1) % maxSize == front
队列为空的条件: rear == front
package queue; import java.util.Scanner; public class CircleQueue { public static void main(String[] args) { //测试一把 System.out.println("测试数组模拟环形队列的案例~~~"); // 创建一个环形队列 CircleArray queue = new CircleArray(4); //说明设置4,其队列有效数据最大是3 char key = ' '; // 接收用户输入 Scanner scanner = new Scanner(System.in);// boolean loop = true; // 输出一个菜单 while (loop) { System.out.println("s(show): 显示队列"); System.out.println("e(exit): 退出程序"); System.out.println("a(add): 添加数据到队列"); System.out.println("g(get): 从队列取出数据"); System.out.println("h(head): 查看队列头的数据"); key = scanner.next().charAt(0);// 接收一个字符 switch (key) { case 's': queue.showQueue(); break; case 'a': System.out.println("输出一个数"); int value = scanner.nextInt(); queue.addQueue(value); break; case 'g': // 取出数据 try { int res = queue.getQueue(); System.out.printf("取出的数据是 %d ", res); } catch (Exception e) { // TODO: handle exception System.out.println(e.getMessage()); } break; case 'h': // 查看队列头的数据 try { int res = queue.headQueue(); System.out.printf("队列头的数据是%d ", res); } catch (Exception e) { // TODO: handle exception System.out.println(e.getMessage()); } break; case 'e': // 退出 scanner.close(); loop = false; break; default: break; } } System.out.println("程序退出~~"); } } class CircleArray { private int maxSize; // 表示数组的最大容量 //front 变量的含义做一个调整:front就指向队列的第一个元素,也就是说arr[front]就是队列的第一个元素 //front 初始值= 0 private int front; //rear 变量的含义做一个调整:rear 指向队列的最后一个元素的后一个位置.因为希望空出一个空间做为约定 //rear 初始值= 0 private int rear; // 队列尾 private int[] arr; // 该数据用于存放数据,模拟队列 public CircleArray(int arrMaxSize) { maxSize = arrMaxSize; arr = new int[maxSize]; } // 判断队列是否满 public boolean isFull() { return (rear + 1) % maxSize == front; } // 判断队列是否为空 public boolean isEmpty() { return rear == front; } // 添加数据到队列 public void addQueue(int n) { // 判断队列是否满 if (isFull()) { System.out.println("队列满,不能加入数据~"); return; } // 直接将数据加入 arr[rear] = n; // 将rear后移,这里必须考虑取模 rear = (rear + 1) % maxSize; } // 取数据 public int getQueue() { // 判断队列是否为空 if (isEmpty()) { // 抛出异常 throw new RuntimeException("队列空,不能取数据~"); } //这里需要分析出 front 是指向队列的第一个元素 //1. 先把 front 对应的值保留到一个临时变量 //2. 将 front 后移,考虑取模 //3. 将临时保存的变量返回 int value = arr[front]; front = (front + 1) % maxSize; return value; } // 显示队列所有数据 public void showQueue() { // 遍历 if (isEmpty()) { System.out.println("队列空的,没有数据~~"); return; } // 思路:从front开始遍历,遍历多少个元素 for (int i = front; i < front + size(); i++) { System.out.printf("arr[%d]=%d ", i % maxSize, arr[i % maxSize]); } } // 求出当前队列有效数据个数 public int size() { // rear = 2 // front = 1 // maxSize = 3 return (rear + maxSize - front) % maxSize; } // 显示队列的数据,注意不是取出数据 public int headQueue() { // 判断 if (isEmpty()) { throw new RuntimeException("队列空的,没有数据~~"); } return arr[front]; } } -