机考刷机-树相关

不同的二叉搜索树

问题

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

方法一：动态规划

题目要求是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：

1. G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。

2. F(i, n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。

可见，G(n)是我们求解需要的函数。
稍后我们将看到，G(n)可以从 F(i, n)得到，而 F(i, n) 又会递归地依赖于G(n)。

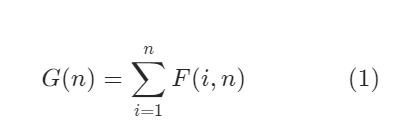
将节点i作为根节点
则 左子序列构建左子树的数量为 G（i-1）,右子序列构建右子树的数量为 G (n-i)
F(i,n)=G(i−1)⋅G(n−i) 公式(2)
将公式 (1)(1)，(2)(2) 结合，可以得到 G(n)的递归表达式：

public class TwoTreeNumber {
    public int numTrees(int n) {
        int[] G = new int[n + 1];
        G[0] = 1;
        G[1] = 1;

        for (int i = 2; i <= n; ++i) {
            for (int j = 1; j <= i; ++j) {
                G[i] += G[j - 1] * G[i - j];
            }
        }
        return G[n];
    }
}