巴特沃斯滤波器的特点:
1、通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
2、在振幅的对数对角频率的波特图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
测试代码:
% ButterWorthFilter.m
% 巴特沃夫滤波器的设计
%
clear;
close all;
clc;
fs = 1000; %Hz 采样频率
Ts = 1/fs;
N = 1000; %序列长度
t = (0:N-1)*Ts;
delta_f = 1*fs/N;
f1 = 50;
f2 = 100;
f3 = 200;
f4 = 400;
x1 = 2*0.5*sin(2*pi*f1*t);
x2 = 2*0.2*sin(2*pi*f2*t);
x3 = 2*0.3*sin(2*pi*f3*t);
x4 = 2*0.6*sin(2*pi*f4*t);
x = x1 + x2 + x3 + x4; %待处理信号由四个分量组成
X = fftshift(abs(fft(x)))/N;
X_angle = fftshift(angle(fft(x)));
f = (-N/2:N/2-1)*delta_f;
figure(1);
subplot(3,1,1);
plot(t,x);
title('原信号');
subplot(3,1,2);
plot(f,X);
grid on;
title('原信号频谱幅度特性');
subplot(3,1,3);
plot(f,X_angle);
title('原信号频谱相位特性');
grid on;
%设计一个巴特沃夫低通滤波器,要求把50Hz的频率分量保留,其他分量滤掉
wp = 65/(fs/2); %通带截止频率,取50~100中间的值,并对其归一化
ws = 85/(fs/2); %阻带截止频率,取50~100中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N1 wc1 ] = buttord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = butter(N1,wc1,'low');
%滤波
filter_lp_s = filter(b,a,x);
X_lp_s = fftshift(abs(fft(filter_lp_s)))/N;
X_lp_s_angle = fftshift(angle(fft(filter_lp_s)));
figure(2);
freqz(b,a); %滤波器频谱特性
figure(3);
subplot(3,1,1);
plot(t,filter_lp_s);
grid on;
title('低通滤波后时域图形');
subplot(3,1,2);
plot(f,X_lp_s);
title('低通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_lp_s_angle);
title('低通滤波后频域相位特性');
%设计一个高通滤波器,要求把400Hz的频率分量保留,其他分量滤掉
wp = 350/(fs/2); %通带截止频率,取200~400中间的值,并对其归一化
ws = 380/(fs/2); %阻带截止频率,取200~400中间的值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N2 wc2 ] = buttord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = butter(N2,wc2,'high');
%滤波
filter_hp_s = filter(b,a,x);
X_hp_s = fftshift(abs(fft(filter_hp_s)))/N;
X_hp_s_angle = fftshift(angle(fft(filter_hp_s)));
figure(4);
freqz(b,a); %滤波器频谱特性
figure(5);
subplot(3,1,1);
plot(t,filter_hp_s);
grid on;
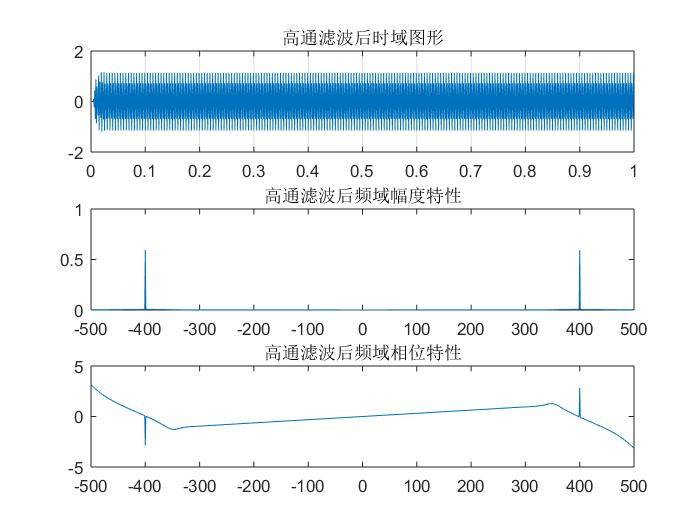
title('高通滤波后时域图形');
subplot(3,1,2);
plot(f,X_hp_s);
title('高通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_hp_s_angle);
title('高通滤波后频域相位特性');
%设计一个带通滤波器,要求把50Hz和400Hz的频率分量滤掉,其他分量保留
wp = [65 385 ] / (fs/2); %通带截止频率,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375 ] / (fs/2); %阻带截止频率,50~100、200~400中间各取一个值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N3 wn ] = buttord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = butter(N3,wn,'bandpass');
%滤波
filter_bp_s = filter(b,a,x);
X_bp_s = fftshift(abs(fft(filter_bp_s)))/N;
X_bp_s_angle = fftshift(angle(fft(filter_bp_s)));
figure(6);
freqz(b,a); %滤波器频谱特性
figure(7);
subplot(3,1,1);
plot(t,filter_bp_s);
grid on;
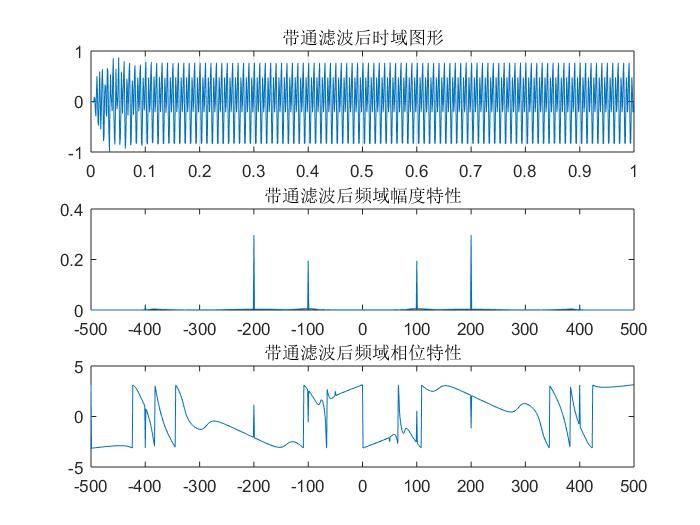
title('带通滤波后时域图形');
subplot(3,1,2);
plot(f,X_bp_s);
title('带通滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bp_s_angle);
title('带通滤波后频域相位特性');
%设计一个带阻滤波器,要求把50Hz和400Hz的频率分量保留,其他分量滤掉
wp = [65 385 ] / (fs/2); %通带截止频率?,50~100、200~400中间各取一个值,并对其归一化
ws = [75 375 ] / (fs/2); %阻带截止频率?,50~100、200~400中间各取一个值,并对其归一化
alpha_p = 3; %通带允许最大衰减为 db
alpha_s = 20;%阻带允许最小衰减为 db
%获取阶数和截止频率
[ N4 wn ] = buttord( wp , ws , alpha_p , alpha_s);
%获得转移函数系数
[ b a ] = butter(N4,wn,'stop');
%滤波
filter_bs_s = filter(b,a,x);
X_bs_s = fftshift(abs(fft(filter_bs_s)))/N;
X_bs_s_angle = fftshift(angle(fft(filter_bs_s)));
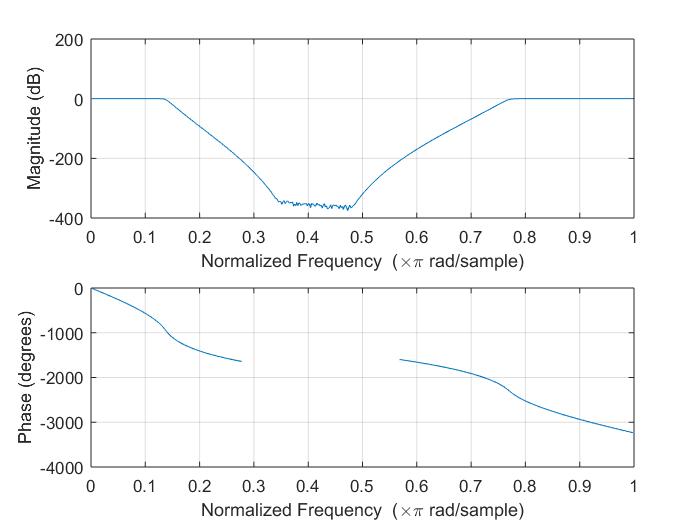
figure(8);
freqz(b,a); %滤波器频谱特性
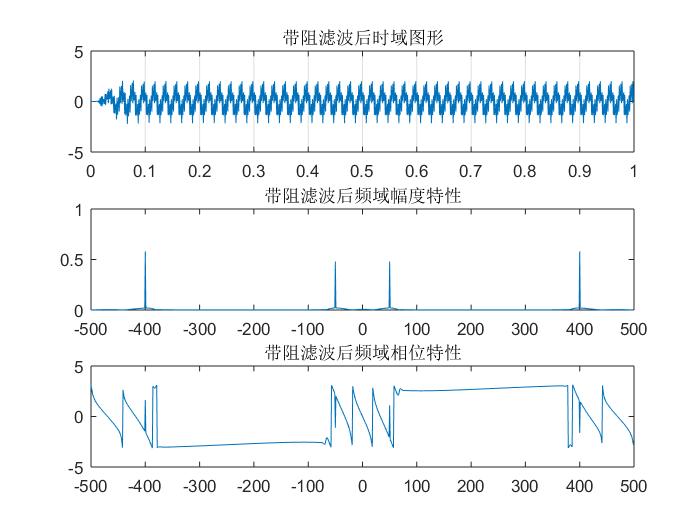
figure(9);
subplot(3,1,1);
plot(t,filter_bs_s);
grid on;
title('带阻滤波后时域图形');
subplot(3,1,2);
plot(f,X_bs_s);
title('带阻滤波后频域幅度特性');
subplot(3,1,3);
plot(f,X_bs_s_angle);
title('带阻滤波后频域相位特性');
效果:
原始信号:

生成的低通滤波器和滤波后的效果:

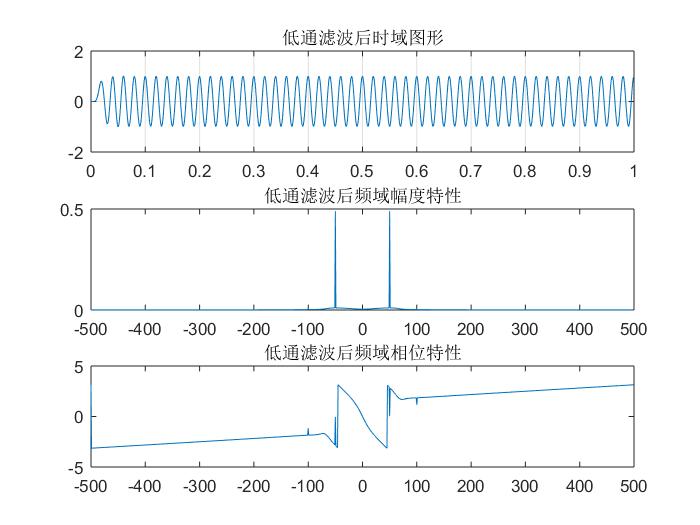
生成的高通滤波器和滤波后的结果:
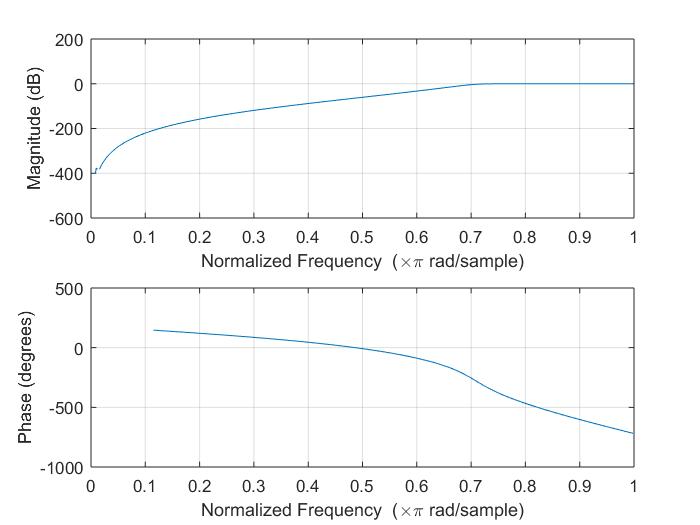
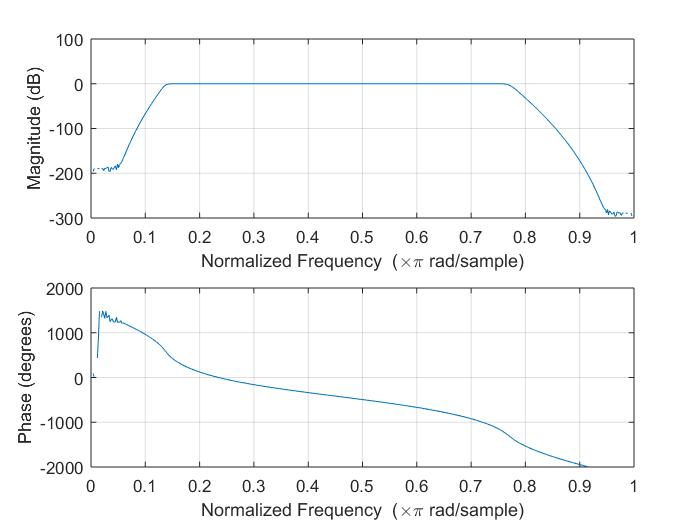
生成的带通滤波器和滤波后的结果:
生成的带阻滤波器和滤波后的结果: