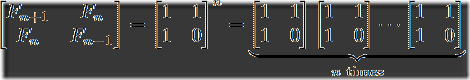http://poj.org/problem?id=3070
方法:
divide and conquer,类似于求幂
矩阵求幂
复杂度:O(logn)
| F(n+1) F(n) | = | 1 1 |^n
| F(n) F(n-1) | | 1 0 |
矩阵的0次幂是单位矩阵
Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0
9
999999999
1000000000
-1
Sample Output
0
34
626
6875
1: #include <stdio.h>
2:
3: struct Matrix
4: {
5: Matrix( int a=1, int b=1, int c=1, int d=0 ):a11(a),a12(b),a21(c),a22(d){}
6: void set( int a=1, int b=1, int c=1, int d=0 ){a11=a;a12=b;a21=c;a22=d;}
7: int a11; int a12; int a21; int a22;
8: };
9:
10: Matrix MatrixMultiply( Matrix& a, Matrix& b )
11: {
12: Matrix result ;
13: result.a11 = ( a.a11*b.a11 + a.a12*b.a21 ) % 10000 ;
14: result.a12 = ( a.a11*b.a12 + a.a12*b.a22 ) % 10000 ;
15: result.a21 = ( a.a21*b.a11 + a.a22*b.a21 ) % 10000 ;
16: result.a22 = ( a.a21*b.a12 + a.a22*b.a22 ) % 10000 ;
17:
18: return result ;
19: }
20:
21: Matrix Fibonacci( Matrix& a, int n )
22: {
23: Matrix result ;
24: if( n==0 )
25: {
26: result.set(1,0,0,1) ;
27: return result ;
28: }
29: if( n==1 )
30: return result ;
31:
32: Matrix tmp ;
33: tmp = Fibonacci( a, n/2 ) ;
34: result = MatrixMultiply( tmp, tmp ) ;
35: if( n%2==0 )
36: return result;
37: else
38: return MatrixMultiply(a,result) ;
39: }
40:
41: void run3070()
42: {
43: Matrix a,result ;
44: int n ;
45:
46: while( scanf( "%d", &n ) && n!=-1 )
47: {
48: result = Fibonacci( a, n ) ;
49: printf( "%d\n", result.a12 ) ;
50: }
51: }