先mk一个容斥原理详解
容斥原理大概就是 :
要计算几个集合并集的大小,我们要先将所有单个集合的大小计算出来,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推,一直计算到所有集合相交的部分。
引用叶学长的例子:
基本思想
A和B出现至少一人的概率(或方案数等)=A出现的概率+B出现的概率-两人同时出现的概率。
更常见的应用:
A和B都不出现的概率=1-至少出现一人的概率,然后再容斥算后面那个东西。
更高级的应用:
n个A全部鸽鸽的概率=1-至少鸽一个的概率+至少鸽两个的概率-......=1-至少鸽奇数个的概率+至少鸽偶数个的概率。
考试时如果感觉有点策不清就画图吧。。。韦恩图是特别重要的解题手段
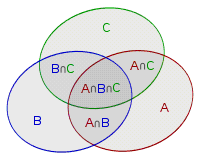
容斥原理基本公式
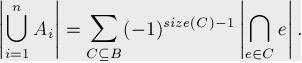
证明看容斥原理详解
我们来看一道题
简化后为:
硬币购物一共有4种硬币。面值分别为c1,c2,c3,c4。某人去商店买东西,去了tot次。每次带di枚ci硬币,买s的价值的东西。请问每次有多少种付款方法。
其中注意数据范围di,s<=100000,tot<=1000。
本题如何用容斥原理:
引用题解的话:
简单来说,就是把重复计算的部分去掉,把多去掉的部分加回来
针对本题而言,就是:
不合法数目=1超出的部分+2超出的部分+……1,2共同超出的部分-2,3共同超出的部分……+1,2,3共同超出的部分……(后面以此类推)
代码实现就比较容易了
贴上代码
#include<bits/stdc++.h>
using namespace std;
#define int long long //这道题不开long long会爆int
int t,k,n,m;
int s;
int ans=0;
int f[100005],c[5],d[5];//f[i]为预处理的完全背包
inline int read() //快读
{
char ch=getchar();
int x=0,q=1;
while(ch>'9' || ch<'0')q=ch==45?-1:q,ch=getchar();
while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^'0'),ch=getchar();
return x*q;
}
inline void work()
{
f[0]=1;
for(int i=1;i<=4;++i)
for(int v=c[i];v<=100000;++v)
f[v]+=f[v-c[i]];
}
inline void dfs(int now,int s,int b)
{
if(s<0) return;
if(now>4)
{
ans+=f[s]*b;
return;
}//剪枝
dfs(now+1,s,b);//求合法的部分
dfs(now+1,s-(d[now]+1)*c[now],-b);//求不合法的部分,b要变号所以乘以-1;
}
signed main()
{
for(int i=1;i<=4;++i)
c[i]=read();
work();
t=read();
while(t)
{
--t;
ans=0;
for(int i=1;i<=4;i++)
d[i]=read();
s=read();
dfs(1,s,1);
printf("%lld
",ans);
}
return 0;
}
总结思路
先预处理f[i]表示在不限制硬币数量的情况下购买价值为i的物品的方案数。于是我们可以跑一个完全背包。
对于硬币个数的限制,考虑容斥:钦定若干种硬币使用di+1次,也就是钦定它超过限制。设被钦定的总费用为x,方案数就是f[s-x]。容斥一下,偶加奇减。
通过容斥原理,可以证明二维前缀和的原理
具体证明为画图,直观的表现出容斥原理的思想。
二维前缀和,有效减少查询统计时的复杂度,每一次查询O(n)O(n)降到O(1),绝对过的了
记住:上加左,减左上,加自己
ans[i][j]=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1];
此题要用二维前缀和优化
优化之后的代码
#include<bits/stdc++.h>
using namespace std;
int t,k,n,m;
long long c[2005][2005],ans[2005][2005];//ans表示二维前缀和
inline void work()
{
c[0][0]=1;
for(int i=1;i<=2000;++i)
{
c[i][0]=1;
for(int j=1;j<=i;++j)
{
c[i][j]=(c[i-1][j]%k+c[i-1][j-1]%k)%k;
ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];//二维前缀和,上加左,减左上。
if(c[i][j]==0)
ans[i][j]++;//加自己
}
ans[i][i+1]=ans[i][i];
}
}
inline int read()
{
char ch=getchar();
int x=0,q=1;
while(ch>'9' || ch<'0')q=ch==45?-1:q,ch=getchar();
while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^'0'),ch=getchar();
return x*q;
}
int main()
{
t=read();
k=read();
work();
while(t)
{
n=read();
m=read();
m=min(n,m);
cout<<ans[n][m]<<endl;
t--;
}
return 0;
}