十大经典排序算法JAVA,大公司必问

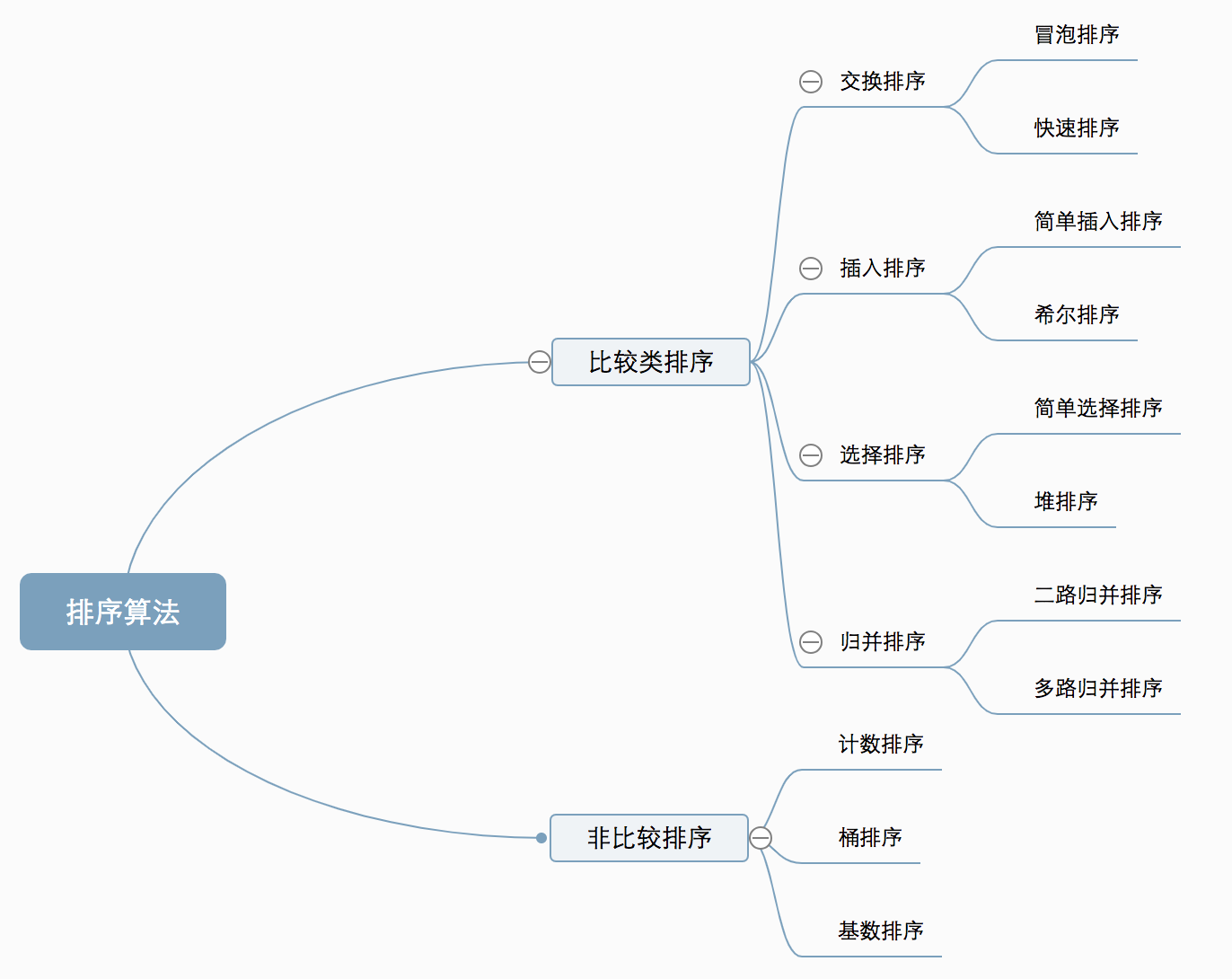
 上面是算法排序的分类，这篇博客用于个人学习使用所以比较简略：

1、冒泡排序（Bubble Sort）

不做太多解释，直接上代码吧；

 

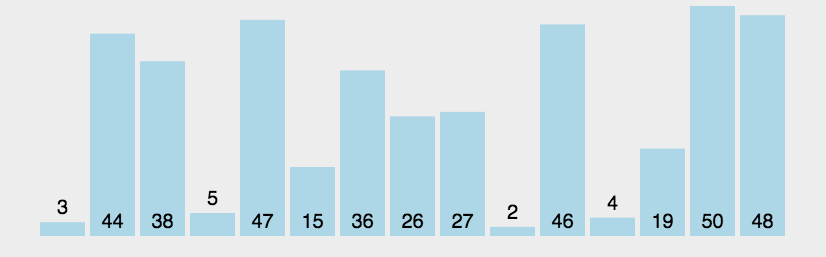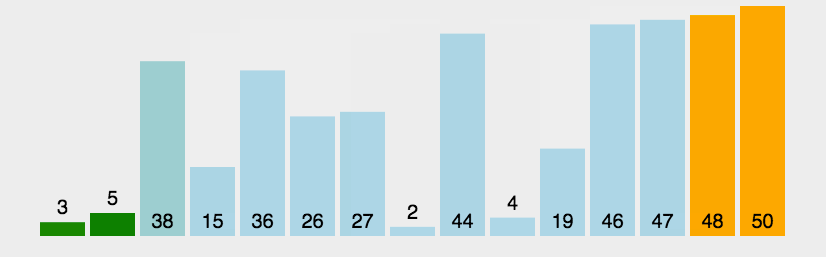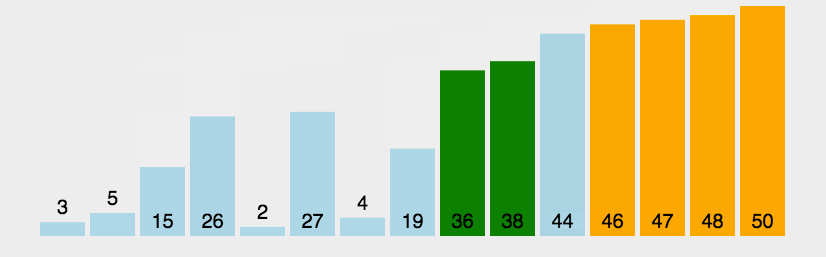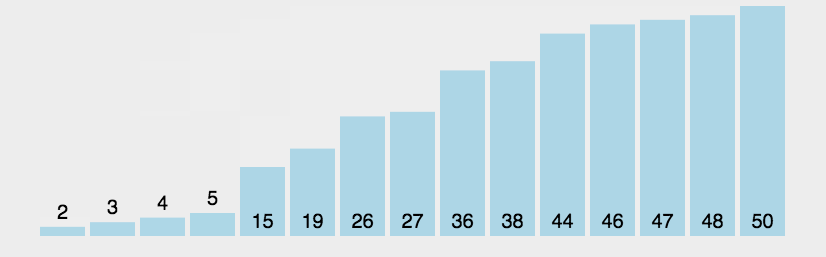
package sort;

import java.util.Scanner;

public class maopao {
    public static void main(String[] args) {
     int[] arr={1,3,4,6,2,10,5,8,7,9};
        for (int i = 0; i <arr.length-1 ; i++) {//第一到第九个数依次和相邻的数比较
            for (int j = 0; j <arr.length-1-i ; j++) {//第一次循环第一个数和后面的数比较。。。
                if (arr[j]>arr[j+1]){
                    int temp=arr[j+1];
                    arr[j+1]=arr[j];
                    arr[j]=temp;
                }
            }
        }
        for (int i = 0; i <arr.length ; i++) {
            System.out.print(arr[i]);
        }
    }
}

2、选择排序（Selection Sort）

选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，交换第一个数和最小值的内容，

存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 

package sort;

import sun.security.util.Length;

public class xuanze {
    public static void main(String[] args) {
        int[] arr = {1, 3, 4, 6, 2, 10, 5, 8, 7, 9};
        int minIndex, temp;//定义最小值的下标
        for (int i = 0; i < arr.length; i++) {
            minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) {//第一次寻找最小的值
                    minIndex = j;
                }
            }
            temp = arr[i];//找到的最小值和第i个数交换
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
        
        for (int i = 0; i <arr.length ; i++) {
            System.out.print(arr[i]);
        }
    }

}

可以思考冒泡的temp和选择的temp为何一个是局部一个是全局：因为选择要交换下标对应的数字内容，冒泡最好为空

3、插入排序（Insertion Sort）

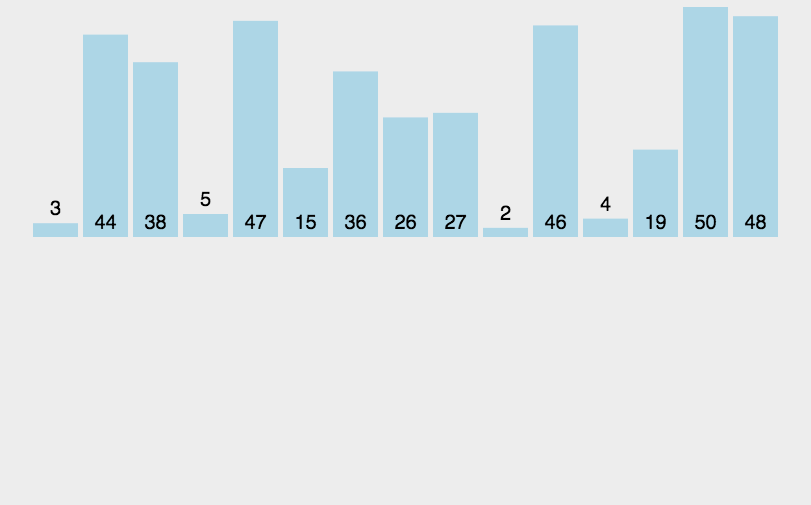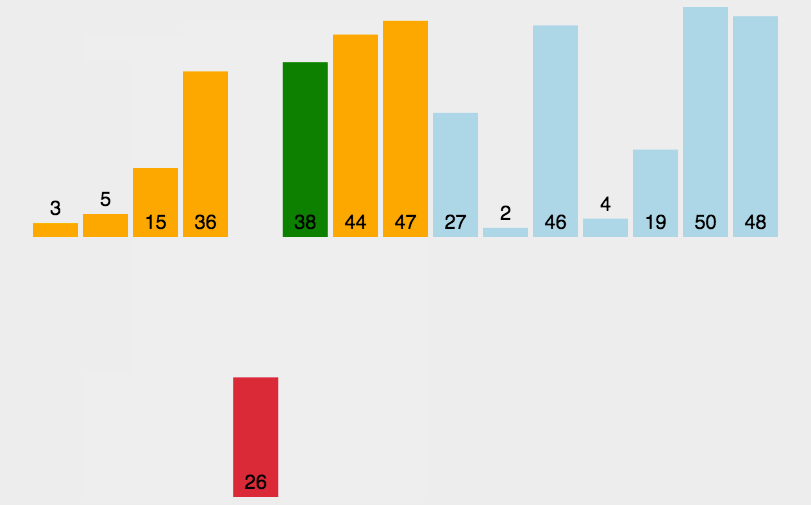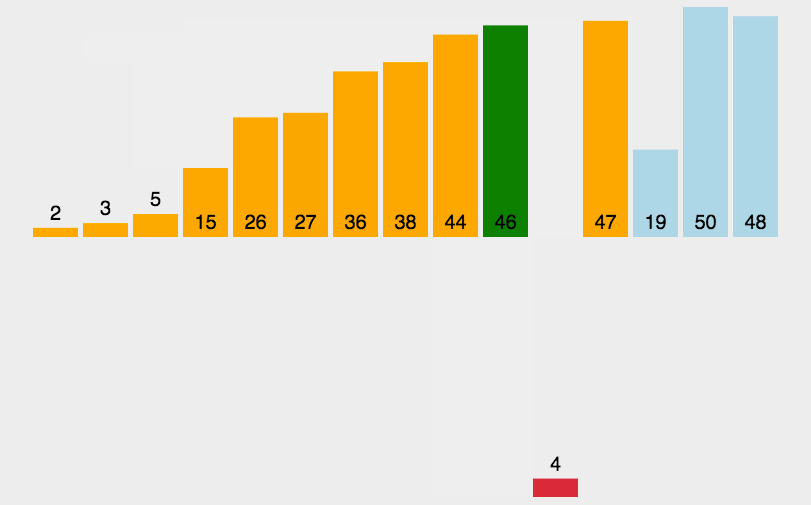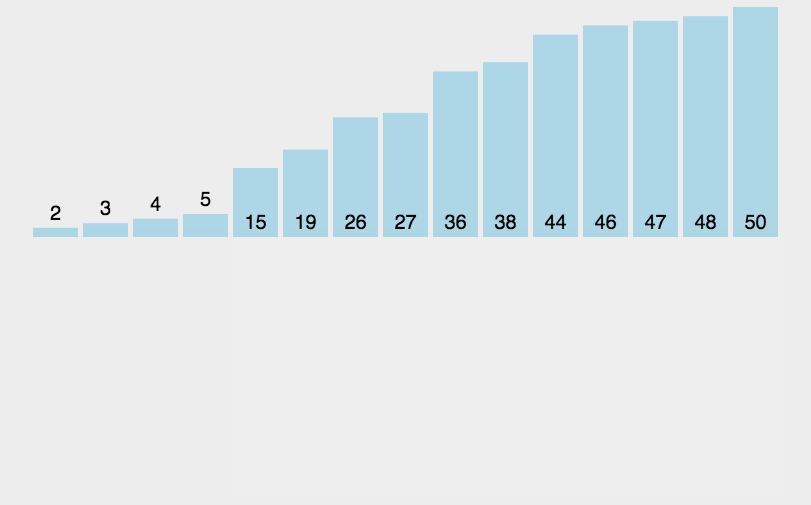
插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

3.1 算法描述

//https://blog.csdn.net/qq_28081081/article/details/80594386

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

• 从第一个元素开始，该元素可以认为已经被排序；
• 取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 如果该元素（已排序）大于新元素，将该元素移到下一位置；
• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 将新元素插入到该位置后；
• 重复步骤2~5。

package sort;
public class charu {
    public static void main(String[] args) {
        int[] arr = {1, 3, 4, 6, 2, 10, 5, 8, 7, 9};
        for (int i = 1; i <arr.length ; i++) {
            for (int j = i; j >0 ; j--) {
                if (arr[j]<arr[j-1]){
                    int temp=arr[j-1];
                    arr[j-1]=arr[j];
                    arr[j]=temp;
                }
            }
        }
        for (int i = 0; i <arr.length ; i++) {
            System.out.print(arr[i]);
        }
    }
}

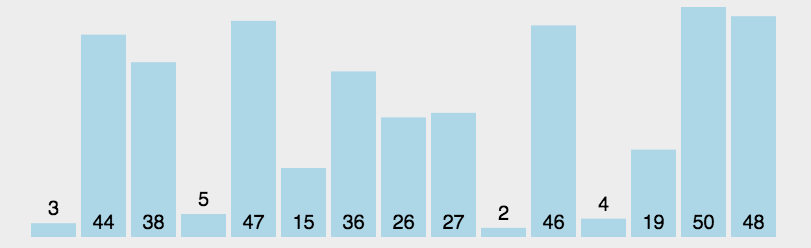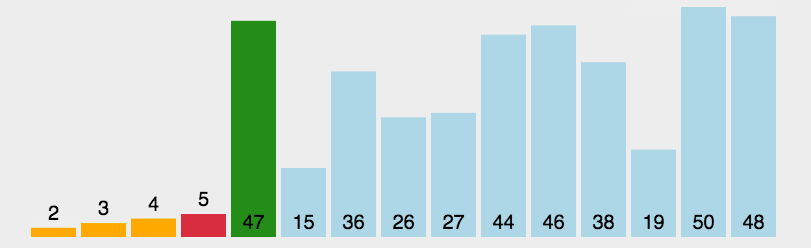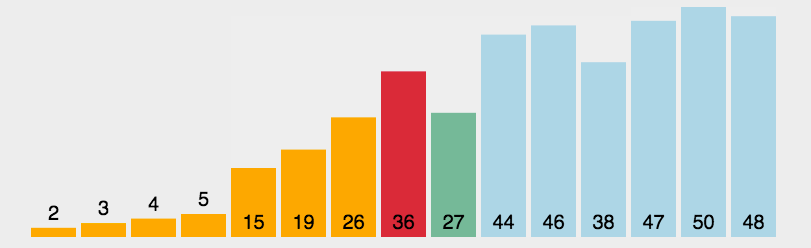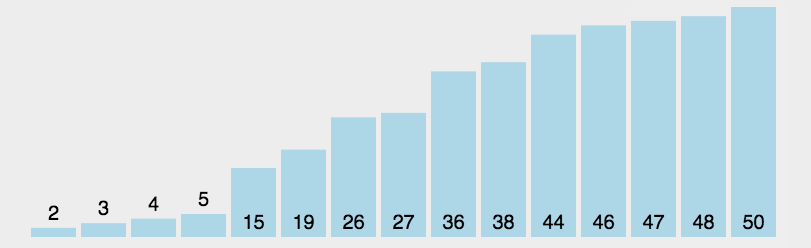
4、希尔排序（Shell Sort）

https://blog.csdn.net/qq_39207948/article/details/80006224

希尔排序

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。

基本思想

设待排序元素序列有n个元素
1.取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列
2.每间隔increment取一个元素，并放在同一个子序列中，对每个子序列实行直接插入排序。
3.缩小间隔increment
4.重复上述子序列划分和排序工作。直到increment=1，即所有元素放在同一个子序列中进行最后的排序。

---

简单点~

假设有数组：{a0,a1,a2,a3,a4,a5,a6,a7,a8,a9}
此时 n = 10
1.一般情况下，我们取increment为：10/2 = 5,则此时：{a0,a5}、{a1,a6}、{a2,a7}、{a3,a8}、{a4,a9}这五组就是该数组的子序列,分别对这些子序列进行插入排序。
2.我们再取increment为：5/2 = 2，则此时：{a0,a2,a4,a6,a8}和{a1,a3,a5,a7,a9}这两组就是该数组的子序列,分别对这两个序列进行插入排序。
3.我们再取increment为：2/1 = 1,则此时：{a0,a1,a2,a3,a4,a5,a6,a7,a8,a9}所有元素都在同一个子序列中。
4.此时对其进行插入排序，因为有前面的工作基础，大多数元素已经基本有序，所以排序速度仍然很快。
从上面我们可以看到，增量increment是在逐渐减小的，所以这个方法我们也叫它为：缩小增量排序。

---

图示：

 

image

---

代码实现

public class ShellSort {
public static void main(String[] args) {
    int[] arr = {4,6,7,4,3,7,34,95,33,67,88,33};
    shellSort(arr);
    System.out.println(Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
    int n = arr.length;
    int increment = n/2;
    for(;increment>0;increment/=2) {
        //下面这段代码和插入排序相同，只是这里的间隔是increment
        //直接插入排序的间隔是1
        int i = increment;
        for(;i<arr.length;i++) {
            int temp = arr[i];
            int t = i-increment;
            while(t >= 0 && arr[t] > temp) {
                arr[i] = arr[t];
                t -= increment;
            }
            arr[t+increment] = temp;
            
        }
    }
}

https://www.runoob.com/w3cnote/merge-sort.html

5、归并排序（Merge Sort）

https://blog.csdn.net/weixin_42038639/article/details/90084348

public class MergeSort {
    public static void main(String[] args) {
        int[] ans = {6, 8, 4, 4, 6, 36, 673, 13, 6, 7, 3, 4, 6, 8, 3, 7, 5, 7, 9, 5};
        System.out.print("原数组：");
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i]+",");
        }
        System.out.println();
        mergeSort(ans);
        System.out.print("归并排序之后的数组：");
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i]+",");
        }
    }

    //sort方法的驱动程序
    private static void mergeSort(int[] ans) {
        sort(ans, 0, ans.length - 1);
    }

    //将tmp和Cctr当做参数传入，方便调用merge方法时获得这两个参数
    private static void sort(int[] ans, int left, int right) {
        int mid = (left + right) / 2;
        //当分到只剩下一个元素的情况,则退出递归程序
        if (left >= right) {
            return;
        }
        sort(ans, left, mid);
        sort(ans, mid + 1, right);
        merge(ans, left, mid, right);
    }

    private static void merge(int[] ans, int left, int mid, int right) {
        //声明三个计时器
        int Actr = left;
        int Bctr = mid + 1;
        int Cctr = 0;
        int lenA = mid - left + 1;
        int lenB = right - mid;
        //创建临时数组,长度为A，B数组长度之和
        int[] tmp = new int[right - left + 1];
        //循环A，B中长度较短的长度次数的二倍的次数
        while (Actr <= mid && Bctr <= right) {
            if (ans[Actr] <= ans[Bctr]) {
                tmp[Cctr++] = ans[Actr];
                Actr++;
            } else {
                tmp[Cctr++] = ans[Bctr];
                Bctr++;
            }
        }
        //如果左边的还有剩余，将左边剩余的归并
        while (Actr <= mid){
            tmp[Cctr ++] = ans[Actr ++];
        }
        //如果右边的还有剩余，将右边剩余的归并
        while (Bctr <= right){
            tmp[Cctr ++] = ans[Bctr ++];
        }
        //将临时数组更新到原数组
        for (int i = 0; i < tmp.length; i++) {
            ans[left++] = tmp[i];
        }
    }
}