一、排序分类
内排序:指在排序期间数据对象全部存放在内存的排序;
外排序:指在排序期间全部对象个数太多,不能同时存放在内存,必须根据排序过程的要求,不断在内、外存之间移动的排序。
二、直接插入排序思想(Straight Insert Sort)
将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
要点:设立哨兵,作为临时存储和判断数组边界之用。
直接插入排序示例:
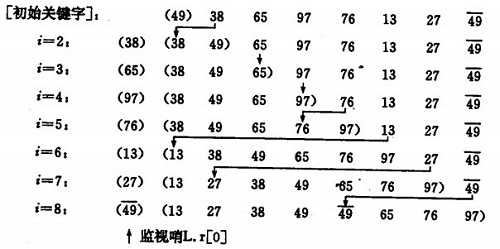
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
- void InsertSort(int a[], int n)
- {
- for(int i= 1; i<n; i++){
- if(a[i] < a[i-1]){ //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入
- int j= i-1;
- int x = a[i]; //复制为哨兵,即存储待排序元素
- a[i] = a[i-1]; //先后移一个元素
- while(x < a[j]){ //查找在有序表的插入位置
- a[j+1] = a[j];
- j--; //元素后移
- }
- a[j+1] = x; //插入到正确位置
- }
- print(a,n,i); //打印每趟排序的结果
- }
- }
三、算法分析:
- 最好情况下,排序前对象已经按照要求的有序。比较次数(KCN):n−1 ; 移动次数(RMN):为0。则对应的时间复杂度为O(n)。
- 最坏情况下,排序前对象为要求的顺序的反序。第i趟时第i个对象必须与前面i个对象都做排序码比较,并且每做1次比较就要做1次数据移动(具体可以从下面给出的代码中看出)。比较次数(KCN):∑n−1i=1i=n(n−1)2≈n22 ; 移动次数(RMN):为∑n−1i=1i=n(n−1)2≈n22。则对应的时间复杂度为O(n2)。
- 如果排序记录是随机的,那么根据概率相同的原则,在平均情况下的排序码比较次数和对象移动次数约为n24,因此,直接插入排序的时间复杂度为O(n2)。
四、算法特点:
- 它是稳定排序,不改变相同元素原来的顺序。
- 它是in-place排序,只需要O(1)的额外内存空间。
- 它是在线排序,可以边接收数据边排序。
- 它跟我们牌扑克牌的方式相似。
- 对小数据集是有效的。