Python语言基础03-分支和循环结构

 本文收录在Python从入门到精通系列文章系列

1. 分支结构

1.1 应用场景

迄今为止，我们写的Python代码都是一条一条语句顺序执行，这种代码结构通常称之为顺序结构。然而仅有顺序结构并不能解决所有的问题，比如我们设计一个游戏，游戏第一关的通关条件是玩家获得1000分，那么在完成本局游戏后，我们要根据玩家得到分数来决定究竟是进入第二关，还是告诉玩家“Game Over”，这里就会产生两个分支，而且这两个分支只有一个会被执行。类似的场景还有很多，我们将这种结构称之为“分支结构”或“选择结构”。

 

1.2 if语句的使用

在Python中，要构造分支结构可以使用if、elif和else关键字。所谓关键字就是有特殊含义的单词，像if和else就是专门用于构造分支结构的关键字，很显然你不能够使用它作为变量名（事实上，用作其他的标识符也是不可以）。

01-单分支

下面的例子中演示了如何构造一个分支结构。

"""

用户身份验证

 

Version: 0.1

Author: along

"""

username = input('请输入用户名: ')

password = input('请输入密码: ')

 

if username == 'along' and password == '12345':

    print('验证通过')

else:

    print('验证失败') 

唯一需要说明的是和C/C++、Java等语言不同，Python中没有用花括号来构造代码块而是使用了缩进的方式来设置代码的层次结构，如果if条件成立的情况下需要执行多条语句，只要保持多条语句具有相同的缩进就可以了，换句话说连续的代码如果又保持了相同的缩进那么它们属于同一个代码块，相当于是一个执行的整体。

 

02-多分支

当然如果要构造出更多的分支，可以使用if…elif…else…结构，例如下面的分段函数求值。

"""

分段函数求值

 

        3x - 5  (x > 1)

f(x) =  x + 2   (-1 <= x <= 1)

        5x + 3  (x < -1)

 

Version: 0.1

Author: along

"""

x = float(input('请输入一个数: '))

if x > 1 :

    y = 3 * x - 5

elif x >= -1 and x <= 1 :

    y = x + 2

else:

    y = 5 * x + 3

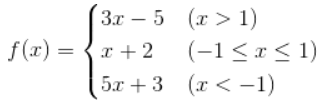
print('f(%.2f) = %.2f' % (x , y))

 

03-嵌套分支

当然根据实际开发的需要，分支结构是可以嵌套的，例如判断是否通关以后还要根据你获得的宝物或者道具的数量对你的表现给出等级（比如点亮两颗或三颗星星），那么我们就需要在if的内部构造出一个新的分支结构，同理elif和else中也可以再构造新的分支，我们称之为嵌套的分支结构，也就是说上面的代码也可以写成下面的样子。

"""

分段函数求值

        3x - 5  (x > 1)

f(x) =  x + 2   (-1 <= x <= 1)

        5x + 3  (x < -1)

 

Version: 0.1

Author: along

"""

x = float(input('x = '))

if x > 1:

    y = 3 * x - 5

else:

    if x >= -1:

        y = x + 2

    else:

        y = 5 * x + 3

print('f(%.2f) = %.2f' % (x, y))

说明： 大家可以自己感受一下这两种写法到底是哪一种更好。在之前我们提到的Python之禅中有这么一句话“Flat is better than nested.”，之所以提倡代码“扁平化”是因为嵌套结构的嵌套层次多了之后会严重的影响代码的可读性，所以能使用扁平化的结构时就不要使用嵌套。

 

1.3 练习

练习1：英制单位英寸与公制单位厘米互换。

参考答案：

"""

英制单位英寸和公制单位厘米互换

 

Version: 0.1

Author: along

"""

value = float(input('请输入长度: '))

unit = input('请输入单位: ')

if unit == 'in' or unit == '英寸':

    print('%f英寸 = %f厘米' % (value, value * 2.54))

elif unit == 'cm' or unit == '厘米':

    print('%f厘米 = %f英寸' % (value, value / 2.54))

else:

    print('请输入有效的单位')

 

练习2：百分制成绩转换为等级制成绩。

要求：如果输入的成绩在90分以上（含90分）输出A；80分-90分（不含90分）输出B；70分-80分（不含80分）输出C；60分-70分（不含70分）输出D；60分以下输出E。

参考答案：

"""

百分制成绩转换为等级制成绩

 

Version: 0.1

Author: along

"""

score = float(input('请输入成绩: '))

if score >= 90:

    grade = 'A'

elif score >= 80:

    grade = 'B'

elif score >= 70:

    grade = 'C'

elif score >= 60:

    grade = 'D'

else:

    grade = 'E'

print('对应的等级是:', grade)

 

练习3：输入三条边长，如果能构成三角形就计算周长和面积。

参考答案：

"""

判断输入的边长能否构成三角形，如果能则计算出三角形的周长和面积

 

Version: 0.1

Author: along

"""

a = float(input('a = '))

b = float(input('b = '))

c = float(input('c = '))

if a + b > c and a + c > b and b + c > a:

    print('周长: %f' % (a + b + c))

    p = (a + b + c) / 2

    area = (p * (p - a) * (p - b) * (p - c)) ** 0.5

    print('面积: %f' % (area))

else:

    print('不能构成三角形')

说明： 上面使用的通过边长计算三角形面积的公式叫做海伦公式。

注意复习下学生时代的等边三角形、直角三角形等知识哦，博主当时就忘了。（捂脸~）

 

2. 循环结构

2.1 应用场景

如果在程序中我们需要重复的执行某条或某些指令，例如用程序控制机器人踢足球，如果机器人持球而且还没有进入射门范围，那么我们就要一直发出让机器人向球门方向奔跑的指令。当然你可能已经注意到了，刚才的描述中不仅仅有需要重复的动作，还需要用到上一章讲的分支结构。再举一个简单的例子，我们要实现一个每隔1秒中在屏幕上打印一次"hello, world"并持续打印一个小时的程序，我们肯定不能够直接把print('hello, world')这句代码写3600遍，如果真的要这样做，那么编程的工作就太无聊乏味了。因此，我们还需要了解一下循环结构，有了循环结构我们就可以轻松的控制某件事或者某些事重复、重复、再重复的去执行。

在Python中构造循环结构有两种做法，一种是for-in循环，一种是while循环。

 

2.2 for-in循环

如果明确的知道循环执行的次数或者要对一个容器进行迭代（后面会讲到），那么我们推荐使用for-in循环。

 

01-案例1

例如下面代码中计算1~100求和的结果（$displaystyle sum limits_{n=1}^{100}n$）。

"""

用for循环实现1~100求和

 

Version: 0.1

Author: along

"""

sum = 0

for a in range(101):

    sum += a

print(sum) 

需要说明的是上面代码中的range(101)可以用来构造一个从0到100的取值范围，这样就可以构造出一个整数的序列并用于循环中，例如：

• range(101)可以产生一个0到100的整数序列。
• range(1, 100)可以产生一个1到99的整数序列。
• range(1, 100, 2)可以产生一个1到99的奇数序列，其中2是步长，即数值序列的增量。

for b in range(10):

    print(b)

for b in range(1,10):

    print(b)

for b in range(1,10,2):

    print(b)

 

02-案例2

知道了这一点，我们可以用下面的代码来实现1~100之间的偶数求和。

"""

用for循环实现1~100之间的偶数求和

 

Version: 0.1

Author: along

"""

sum = 0

for i in range(2,101,2):

    sum += i

print(sum)

 

03-for_in和if结合

也可以通过在循环中使用分支结构的方式来实现相同的功能，代码如下所示。

"""

用for循环实现1~100之间的偶数求和

 

Version: 0.1

Author: along

"""

 

sum = 0

for i in range(1, 101):

    if i % 2 == 0:

        sum += i

print(sum)

 

2.3 while循环

如果要构造不知道具体循环次数的循环结构，我们推荐使用while循环。while循环通过一个能够产生或转换出bool值的表达式来控制循环，表达式的值为True循环继续，表达式的值为False循环结束。

01-无限循环

下面我们通过一个“猜数字”的小游戏（计算机出一个1~100之间的随机数，人输入自己猜的数字，计算机给出对应的提示信息，直到人猜出计算机出的数字）来看看如何使用while循环。

"""

猜数字游戏

计算机出一个1~100之间的随机数由人来猜

计算机根据人猜的数字分别给出提示大一点/小一点/猜对了

 

Version: 0.1

Author: along

"""

import random

 

answer = random.randint(1,100)

counter = 0

# print(answer)

 

while True:

    counter += 1

    number = int(input('请输入一个数字: '))

    if number > answer:

        print('小一点')

    elif number < answer:

        print('大一点')

    else:

        print('恭喜你，答对了')

        break

print('你总共猜了%d次' % counter)

if counter >= 7:

    print('你的智商余额明显不足')

上面的代码中使用了break关键字来提前终止循环，需要注意的是break只能终止它所在的那个循环，这一点在使用嵌套的循环结构（下面会讲到）需要引起注意。除了break之外，还有另一个关键字是continue，它可以用来放弃本次循环后续的代码直接让循环进入下一轮。

 

02-嵌套循环

和分支结构一样，循环结构也是可以嵌套的，也就是说在循环中还可以构造循环结构。下面的例子演示了如何通过嵌套的循环来输出一个九九乘法表。

"""

输出乘法口诀表(九九表)

 

Version: 0.1

Author: along

"""

 

for i in range(1, 10):

    for j in range(1, i + 1):

        print('%d*%d=%d' % (j, i, i * j), end=' ')

    print()

 

2.4 练习

练习1：输入一个正整数判断是不是素数。

提示：素数指的是只能被1和自身整除的大于1的整数。

参考答案：

"""

输入一个正整数判断它是不是素数

 

Version: 0.1

Author: along

"""

from math import sqrt

 

num = int(input('请输入一个正整数: '))

end = int(sqrt(num))

is_prime = True

for x in range(2, end + 1):

    if num % x == 0:

        is_prime = False

        break

if is_prime and num != 1:

    print('%d是素数' % num)

else:

    print('%d不是素数' % num)

 

练习2：输入两个正整数，计算它们的最大公约数和最小公倍数。

参考答案：

"""

输入两个正整数计算它们的最大公约数和最小公倍数

 

Version: 0.1

Author: along

"""

x = int(input('x = '))

y = int(input('y = '))

# 如果x大于y就交换x和y的值

if x > y:

    # 通过下面的操作将y的值赋给x, 将x的值赋给y

    x, y = y, x

# 从两个数中较的数开始做递减的循环

for factor in range(x, 0, -1):

    if x % factor == 0 and y % factor == 0:

        print('%d和%d的最大公约数是%d' % (x, y, factor))

        print('%d和%d的最小公倍数是%d' % (x, y, x * y // factor))

        break

 

练习3：打印如下所示的三角形图案。

注：先"左"直角、”右“直角、最后等腰三角形

*
**
***
****
*****

    *
   **
  ***
 ****
*****

    *
   ***
  *****
 *******
*********

参考答案：

"""

打印三角形图案

 

Version: 0.1

Author: along

"""

row = int(input('请输入行数: '))

for i in range(row):

    for _ in range(i + 1):

        print('*', end='')

    print()

 

 

for i in range(row):

    for j in range(row):

        if j < row - i - 1:

            print(' ', end='')

        else:

            print('*', end='')

    print()

 

for i in range(row):

    for _ in range(row - i - 1):

        print(' ', end='')

    for _ in range(2 * i + 1):

        print('*', end='')

    print()

如果对linux中的分支和循环结构感兴趣的话，请选择传送。