决策树是一种新算法:
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。
决策树算法可用于数据类型:数值型和标称型。
决策树的核心在于选择正确的属性对数据进行划分。选择的标准是数据增益。信息增益:讲无序的数据变得更加有序。
信息增益熵:如果把X分成n个类,每个类的概率为p(i),那么-log(p(i))的期望就是熵。
如果分成1类,则熵为0,表示没有增益。
如果分成两类,各占1半,熵为1;
如果分成4类,各占1/4,则熵为2;
可以直观的感觉分成类越多,熵就越大。
---
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
按照最后一个属性划分,熵为0.97
加上一个元素[1,1,’maybe’],熵就变成1.47
-----
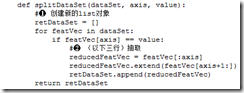
为了计算数据增益,需要定义一个子函数。按照特定的维度,以及维度上的值,划分dataSet。
-----
利用上面的子函数可以选择增益最大的维度。
对每个维度di进行遍历
对di上的value进行切分,得到k个集合
计算一个熵si
选择最大的si,对应的维度就是用来做决策的维度。
-----
每次选择一个维度后,对应的维度就会从数据集消失。然后dataSet分成若干个小集合。如果某个dataSet子集中所有元素label一致,则不需要再次划分。否则继续选择增益最大的属性继续划分。直到构成完整的决策树。