Tensors 张量 类似于NumPy的ndarrays,可以使用GPU进行计算。
概念:张量(Tensor)是一个定义在一些向量空间和一些对偶空间的笛卡儿积上的多重线性映射,其坐标是|n|维空间内,有|n|个分量的一种量, 其中每个分量都是坐标的函数, 而在坐标变换时,这些分量也依照某些规则作线性变换。
(2)在同构的意义下,第零阶张量 (r = 0) 为标量 (Scalar),第一阶张量 (r = 1) 为向量 (Vector), 第二阶张量 (r = 2) 则成为矩阵 (Matrix)。例如,对于3维空间,r=1时的张量为此向量:(x,y,z)。
(3)由于变换方式的不同,张量分成协变张量 (Covariant Tensor,指标在下者)、逆变张量 (Contravariant Tensor,指标在上者)、 混合张量 (指标在上和指标在下两者都有) 三类。
(4)在数学里,张量是一种几何实体,或者说广义上的“数量”。张量概念包括标量、向量和线性算子。
(5)张量可以用坐标系统来表达,记作标量的数组,但它是定义为“不依赖于参照系的选择的”。张量在物理和工程学中很重要。例如在扩散张量成像中,表达器官对于水的在各个方向的微分透性的张量可以用来产生大脑的扫描图。可能最重要的工程上的例子就是应力张量和应变张量了,它们都是二阶张量,对于一般线性材料他们之间的关系由一个四阶弹性张量来决定。
(6)虽然张量可以用分量的多维数组来表示,张量理论存在的意义在于进一步说明把一个数量称为张量的涵义,而不仅仅是说它需要一定数量的有指标索引的分量。特别是,在坐标转换时,张量的分量值遵守一定的变换法则。张量的抽象理论是线性代数分支,现在叫做多重线性代数。
张量构造实例如下:
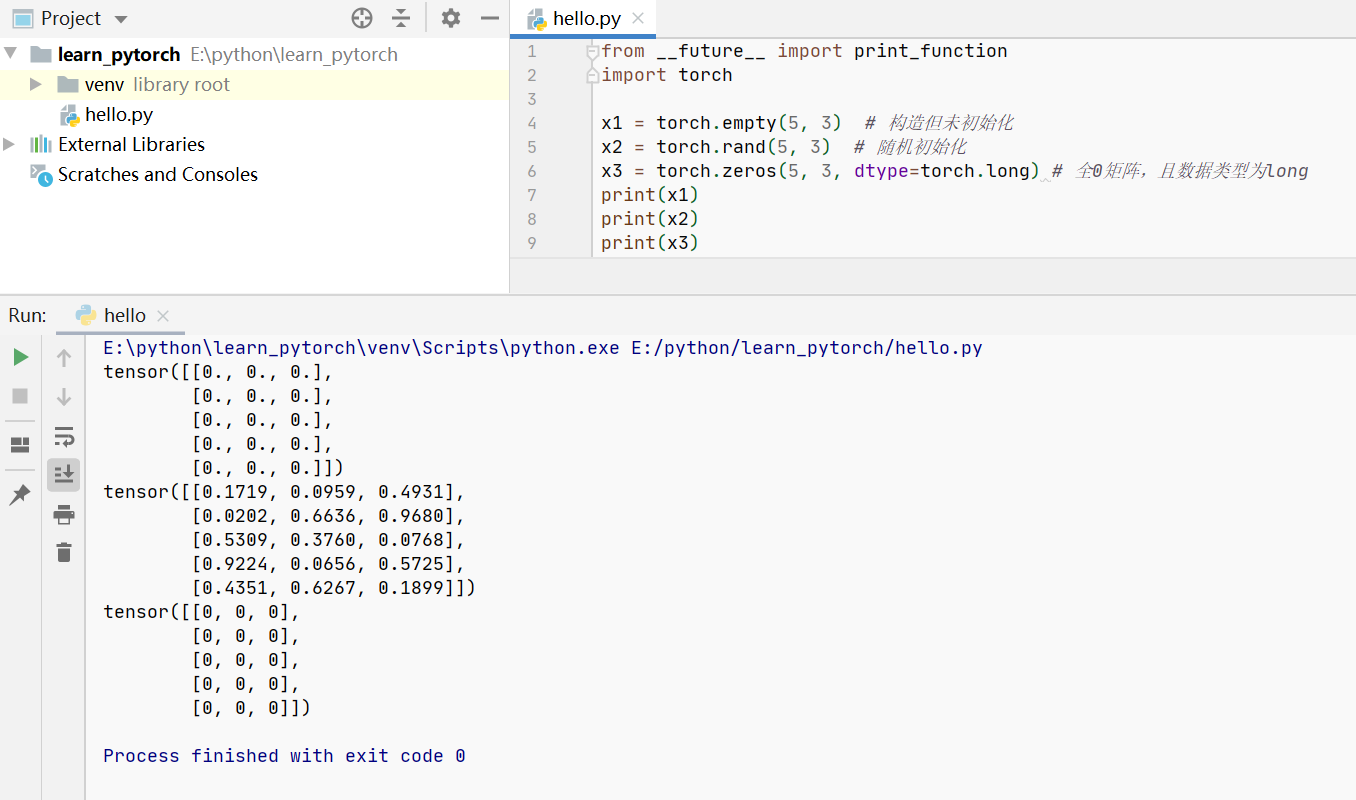
注意:声明一个未初始化的矩阵,它在使用前不包含确定的已知值。创建未初始化的矩阵时,当时分配的内存中的任何值都将显示为初始值。

注意:torch.Size 实际上是一个元组,因此它支持所有元组操作。
更多具体操作
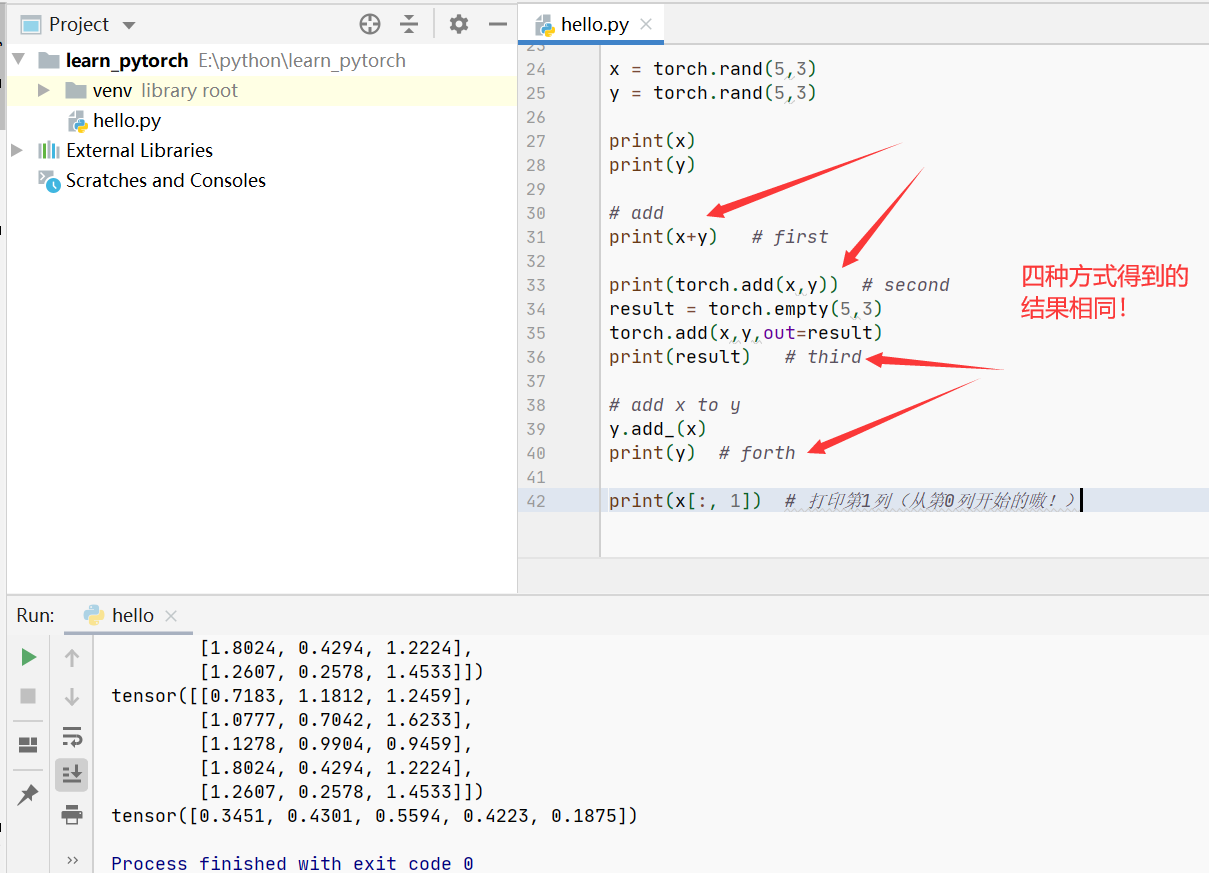
注意:任何使张量自身直接发生变化的操作都用固定"_"。例如:x.copy_(y),x.t_(),将直接改变x。
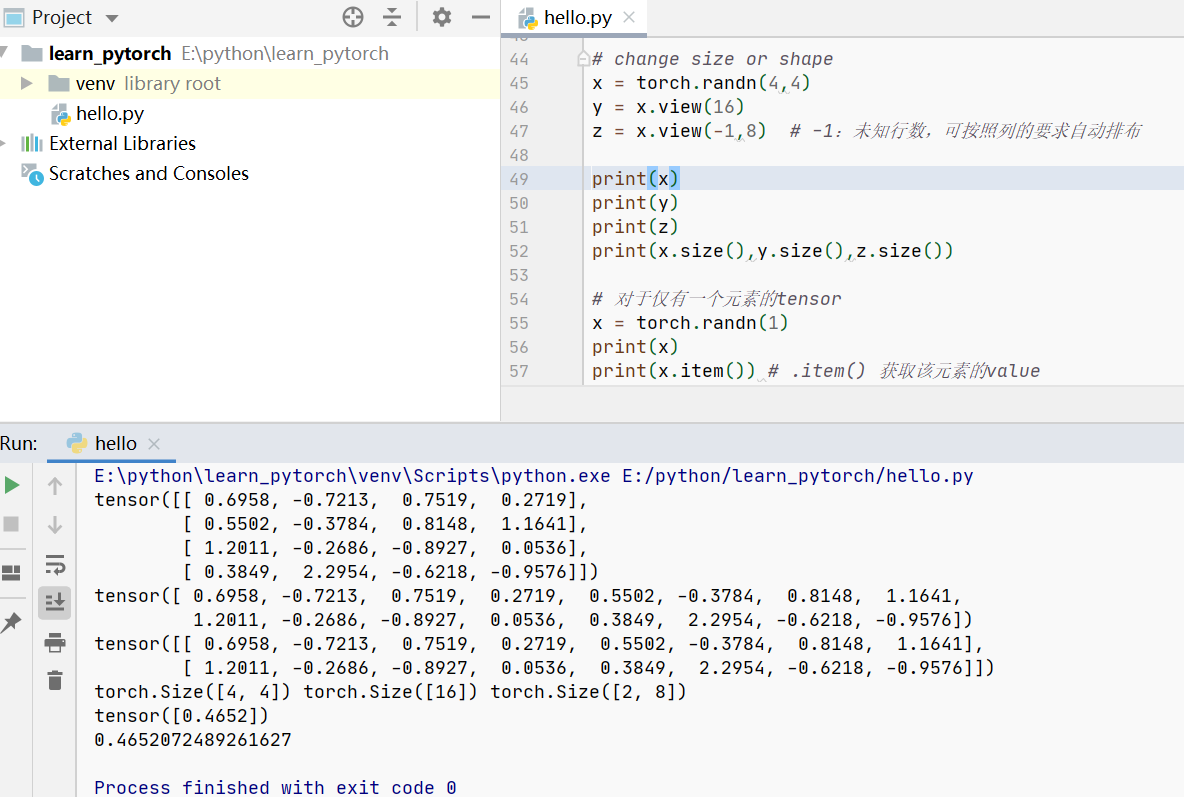
More:https://pytorch.org/docs/stable/torch.html
tensor 和 numpy 之间的转换

注意:Torch Tensor和NumPy数组将共享其基础内存位置(如果Torch Tensor在CPU上),更改一个也将更改另一个。除了CharTensor之外,CPU上的所有张量都支持转换为NumPy并转换回。
CUDA张量
