1.为什么要进行正则化?
机器学习中,如果参数过多,模型会变得复杂,易overfit,即模型在训练样本数据上表现的很好,但在实际测试样本上表现的较差,不具备良好的泛化能力。为了避免过拟合,最常用的一种方法就是使用正则化,从而限制模型参数更多/更大,避免模型的复杂。
2.L1正则化:在原损失函数的基础上加上权重参数的绝对值。
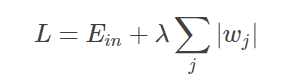
其中,Ein 是未包含正则化项的训练样本误差,λ 是正则化参数,可调。
3.L2正则化:在原来损失函数基础上加上权重参数的平方和。
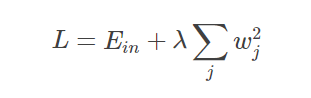
为达到正则化的目的,最简单的方法就是限制w的个数,但这类问题属于NP难问题,即无法求解,所以我们需要寻找一些宽松的限制条件,如:
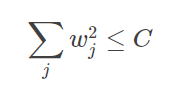
这里对 w 的平方和做数值上界的限定,要求所有w 的平方和不超过参数 C。这时候,我们将目标转换为:最小化训练样本误差 Ein,但是要满足 w 平方和小于 C 这个条件。
4.二者的区别
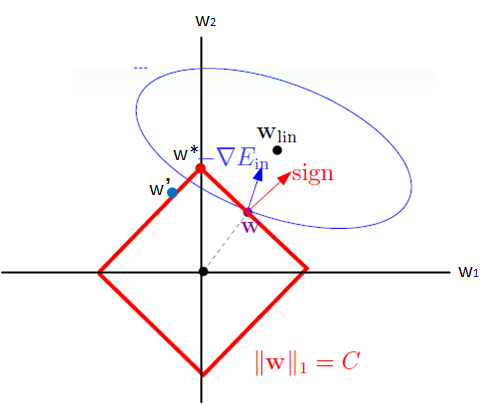
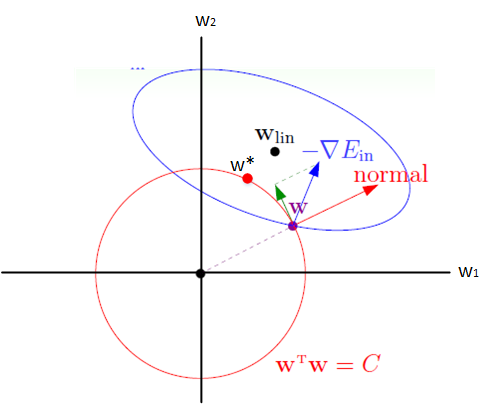
左图为L1正则化,右图为L2正则化。
以二维情况为例,满足正则化条件,即求解椭圆区域与正方形/圆形区域的交点,也就是同时满足了Ein最小化和相应限定条件。
对于L2正则化来说,其限定区域是圆,得到的解w1或w2很大概率是非零的。
而对于L1正则化 来说,其限定区域是正方形,与椭圆区域的交点很大概率是其顶点,即方形的凸点会更接近Ein最优解对应的 wlin 位置,而凸点处必有w1或w2为 0,故得到的解w1或w2为零的概率就很大了。
因此我们说,L1正则化的解具有稀疏性。同理,当扩展到高维情况,L2的限定区域是平滑的,与中心点等距;而L1的限定区域是尖锐的,有凸点。这些凸点更接近Ein的最优解位置,而在这些凸点上,很多wj都为 0。
5.正则化参数λ
正则化是结构风险最小化的一种策略实现,能够有效降低过拟合。此时的损失函数实际上包含了两个方面:训练样本误差和正则化项,此时需要参数 λ 权衡二者。
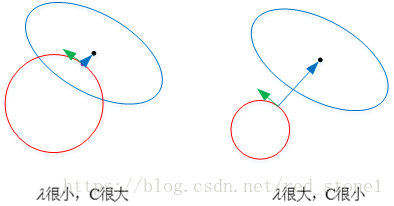
这里以 L2 为例,若 λ 很小,对应 C 值就很大。此时圆形区域很大,能够让 w 更接近 Ein 最优解的位置。若 λ 近似为 0,相当于圆形区域覆盖了最优解位置,这时候,正则化失效,即容易造成过拟合。
相反,若 λ 很大,对应 C 值就很小。此时圆形区域很小,w 离 Ein 最优解的位置较远。w 被限制在一个很小的区域内变化,w 普遍较小且接近 0,可以起到正则化左右。但λ 过大容易造成欠拟合。