java数据结构和算法（一）：二叉树

　　有序数组的查找速度很快，但是插入一个数据项时，就必须先找到插入数据项的位置，然后将后面所有的数据项后移一位，平均要移动N/2次，这是很费时的，删除数据也是。

　　链表的插入和删除很快，只需要改变引用值就行了，但是查找数据却很慢，需要从链表的第一个节点查找到所需要的数据项为止，平均需要比较N/2次。

　　树这种数据结构就具有了两者的优点，数组查找快以及链表插入、删除快。

1.树的定义：

　　树是n个有限个数据点通过连接他们的边组成的具有层次关系的集合。

　　节点高度：从叶节点向上数，连接该节点的边数就是节点的高度

　　节点深度：从根节点往下数，该节点所在的层数就是节点的深度。

　　树中节点高度和深度的最大值就是树的高度和深度。注意：有两种说法，一种是根的深度为0，一种根的深度为1，所以树的深度取决于根节点所在的层数是0还是1。

2.二叉树的性质：

　　（1）两种特殊的树：满二叉树和完全二叉树。在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有的叶节点都在同一层上称为满二叉树；对于一颗具有n个节点的二叉树按层序编号，如果编号为i（0<i<=n）的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同，则称完全二叉树。

　　（2）在二叉树中的第i层上至多有2^(i-1)个节点（i>=1）

　　（3）深度为k的二叉树至多有2^k-1个节点（k>=1）

　　  (4)  对于任何一颗二叉树T，如果其叶子节点数为n0，度为2的节点数为n2，则n0 = n2+1

　　（5）具有n个节点的完全二叉树的深度为|log₂n|+1(|log₂n|为不大于它自身的最大整数)。

3.二叉树的插入、查找和删除

　　这里主要讲二叉搜索树的操作。首先谈二叉搜索树的简单定义：如果节点不为空，有右子节点》根节点》左子节点，满足这样条件的树称为二叉搜索树。

插入：

public void insert(int data){
    if(root==null){
        root = new Node(data);
        return;
    }
    Node temp = root;
    Node pre = new Node();//获取待插入节点的父节点
    while(temp!=null){
        pre = temp;
        if(temp.data==data){
            return;
        }else if(temp.data>data){
            temp = temp.leftnode;
        }else{
            temp = temp.rightnode;
        }
    }
    if(pre.data>data){
        pre.leftnode = new Node(data);
    }else{
        pre.rightnode = new Node(data);
    }

}

查找：

public Node search(int data){
    Node temp = root;
    while(temp!=null){
        if(temp.data==data){
            return temp;
        }else if(temp.data>data){
            temp = temp.leftnode;
        }else{
            temp = temp.rightnode;
        }
    }
    return new Node();
}

删除：

分情况讨论：　

　（1）删除的节点如果没有右节点则直接用左子节点替换。

　（2）否则，如果删除节点的右节点不存在左子树，则直接用该右子节点替换。

　（3）否则，找到右节点的左子树中最左的节点替换被删除的节点，然后将替换节点的右子节点放到替换节点的位置。

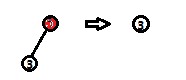
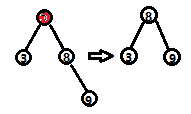
 （1）第一种情况   　　　　　　（2）第二种情况

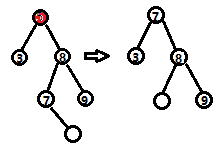
 （3）第三种情况

public boolean delete(int data){
        Node temp = root;
        Node pre = new Node();
        pre.leftnode = root;
        byte state = 0;　　　　　　　　　　　　　　 // 0代表左子节点，1代表右子节点
        while(temp!=null&&temp.data!=data){    //找到待删除的节点
            pre = temp;
            if(temp.data>data){
                temp = temp.leftnode;
                state = 0;
            }else{
                temp = temp.rightnode;
                state = 1;
            }
        }
        if(temp==null) return false;

        Node templ = temp.leftnode;　　　　　　//保存待删除节点的左子树和右子树
        Node tempr = temp.rightnode;

        if(tempr==null){　　　　　　　　　　　　//第一种情况
            connectNode(pre,templ,state);
        }else if(tempr.leftnode==null){　　　//第二种情况
            connectNode(pre,tempr,state);
            tempr.leftnode = templ;
        }else{　　　　　　　　　　　　　　　　　　//第三种情况
            Node pre2 = tempr;
            temp = pre2.leftnode;
            while(temp.leftnode!=null){
                pre2 = temp;
                temp = temp.leftnode;
            }
            pre2.leftnode = temp.rightnode;

            temp.leftnode = templ;
            temp.rightnode = tempr;
            if(pre.leftnode==root) root = temp;
            connectNode(pre,temp,state);
        }
        return true;
    }

 private void connectNode(Node pre, Node node, byte state) {

    if(state==0){
        pre.leftnode = node;
    }else{
        pre.rightnode = node;
    }
}

　　通过上面的删除分类讨论，我们发现删除其实是挺复杂的，那么其实我们可以不用真正的删除该节点，只需要在Node类中增加一个标识字段isDelete，当该字段为true时，表示该节点已经删除，反正没有删除。那么我们在做比如find()等操作的时候，要先判断isDelete字段是否为true。这样删除的节点并不会改变树的结构。

4.遍历二叉树

（1）前序遍历：父节点=》左子节点=》右子节点

递归算法：

public void beforeOrder(Node node){
        if(node==null){
            return;
        }
        System.out.println(node.data);
        beforeOrder(node.leftnode);
        beforeOrder(node.rightnode);
    }

非递归算法：

    public void beforeOrder2(Node node){
        Stack<Node> stack = new Stack<>();
        stack.push(node);
        while(!stack.isEmpty()){
            Node pop = stack.pop();
            if (pop==null) continue;
            System.out.println(pop.data);
            stack.push(pop.rightnode);
            stack.push(pop.leftnode);
        }

    }

（2）中序遍历：左子节点=》父节点=》右子节点

递归算法：

public void inOrder(Node node){
    if(node==null){
        return;
    }
    inOrder(node.leftnode);
    System.out.println(node.data);
    inOrder(node.rightnode);
}

非递归算法：

public void inOrder2(Node node){
    Stack<Node> stack = new Stack<>();
    Node cur = node;
    while(!stack.isEmpty()||cur!=null){
        while(cur!=null){
            stack.push(cur);
            cur = cur.leftnode;
        }
        Node pop = stack.pop();
        System.out.println(pop.data);
        if(pop.rightnode==null) continue;
        cur = pop.rightnode;
    }
}

（3）后序遍历：左子节点=》右字节点=》父节点

递归算法：

public void afterOrder(Node node){
    if(node==null){
        return;
    }
    afterOrder(node.leftnode);
    afterOrder(node.rightnode);
    System.out.println(node.data);
}

非递归算法：

public void afterOrder2(Node node){
    Stack<Node> stack = new Stack<>();
    stack.push(node);
    List<Node> mylist = new ArrayList<>();
    while(!stack.isEmpty()){
        Node pop = stack.pop();
        if (pop==null) continue;
        mylist.add(pop);
        stack.push(pop.leftnode);
        stack.push(pop.rightnode);
    }
    Collections.reverse(mylist);
    for (Node node1 : mylist) {
        System.out.println(node1.data);
    }
}

（4）层次遍历

public void levelOrder(Node node){
    Queue<Node> queue = new LinkedList<>();
    queue.offer(node);
    while(!queue.isEmpty()){
        int size = queue.size();
        while(size-->0){
            Node node1 = queue.poll();
            if(node1==null){
                continue;
            }
            System.out.println(node1.data);
            queue.offer(node1.leftnode);
            queue.offer(node1.rightnode);
        }
    }
}

5.效率分析

　　在插入的数据是无序的情况下，插入的效率是logN;在二叉树是平衡树的情况下，删除、查找的效率都为logN；但是树的遍历效率比较低。