一、概述
层次分析法是一种实用的多准则决策方法,它把一个复杂问题表示为有序的递阶层次结构,通过人们的判断对决策方案的优劣进行排序。这是一种将定性分析和定量分析相结合的评价决策方法,特别适合于社会经济系统问题的决策分析。
二、步骤
1)对构成决策问题的各种要素建立多级(多层次)递阶结构模型;
2)对同一层次(等级)的要素以上一级的要素为准则进行两两比较,并根据评定尺度确定其相对重要程度,最后据此建立判断矩阵。
3)通过一定计算,确定各要素的相对重要度。
4)通过综合重要度的计算,对所有的替代方案进行优先排序,从而为决策人选择最优方案提供科学的决策依据。
三、具体实施
1.明确问题
2.建立多级递阶层次结构
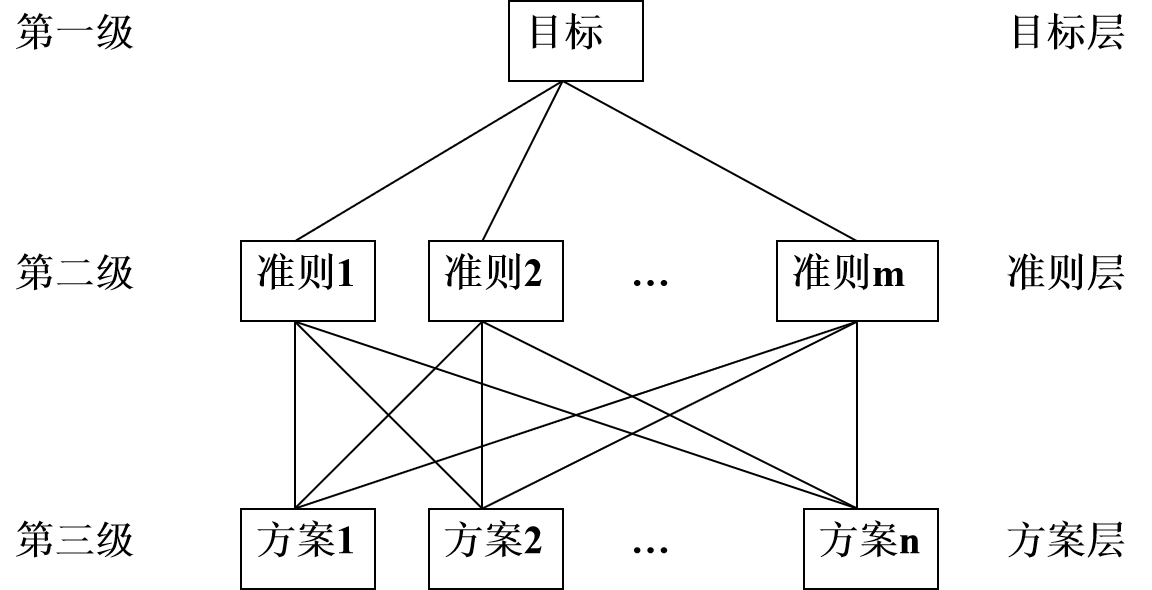
3.构造两两比较判断矩阵
4.相对重要度计算
1)和积法
2)方根法
5.一致性检验
四、具体举例和代码
有一个毕业生为挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生,该毕业生考虑的因素有6个,研究课题、发展前途、待遇、同事情况、地理位置和单位名气。
那么这六个因素就是准则层,三个单位就是方案层,最后要求的就是应该去哪个单位。
1)准则层判断矩阵(主观性)

2)方案层判断矩阵(主观性)
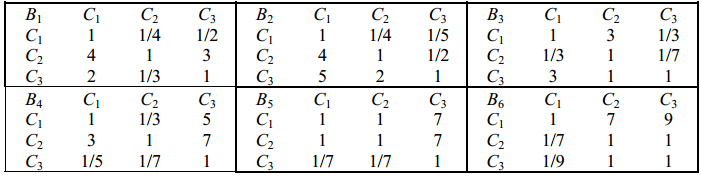
clc,clear
fid=fopen('txt3.txt','r');
n1=6;n2=3; a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp];%读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1)
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2) %读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标 %查表
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
其中,txt3的内容如下:
1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1
1 1/4 1/2
4 1 3
2 1/3 1
1 1/4 1/5
4 1 1/2
5 2 1
1 3 1/3
1/3 1 1/7
3 7 1
1 1/3 5
3 1 7
1/5 1/7 1
1 1 7
1 1 7
1/7 1/7 1
1 7 9
1/7 1 1
1/9 1 1