归并排序
描述:
归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。
合并:
将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
分析演示:
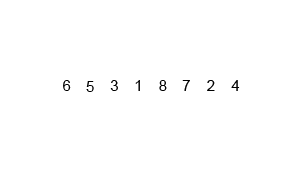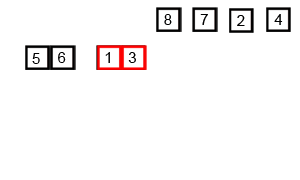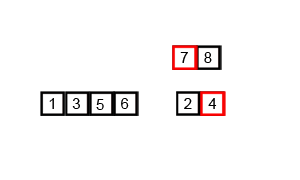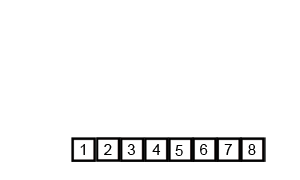
时间复杂度:
最优时间复杂度: O(nlogn)
最坏时间复杂度: O(nlogn)
描述:
归并排序只有一种情况, 所以最优和最坏的复杂度是一样的
分析:
归并排序是由两部分组成的: 拆分, 合并
拆分:
将列表一分为二, 一直拆, 直到被拆分为一个个长度为一的小列表, 每次拆一半, 拆n次, 就会把列表拆分完
因此: 分析的时间复杂度为 O(log2^n)
合并:
合并: 先比较左右两个列表内的元素, 然后进行归位, 也就是合并
因此: 合并的时间复杂度为 O(n)
优化:
O(T) = O(n * log2^n) = O(nlogn)
稳定性: 稳定
描述:
因为列表拆分与合并都是由左至右依次执行的, 合并的判断条件是, 如果左列表的元素小于等于右列表的元素, 将元素添加到新列表内, 如果两个元素相等, 左侧的元素先添加到新的列表内, 相对顺序并没有改变
代码:
简洁版:

def merge_sort(Li): n = len(Li) if n <= 1: return Li mid = n // 2 left_Li = merge_sort(Li[:mid]) right_li = merge_sort(Li[mid:]) left_pointer, right_pointer = 0, 0 result = [] while left_pointer < len(left_Li) and right_pointer < len(right_li): if left_Li[left_pointer] <= right_li[right_pointer]: result.append(left_Li[left_pointer]) left_pointer += 1 else: result.append(right_li[right_pointer]) right_pointer += 1 result += left_Li[left_pointer:] result += right_li[right_pointer:] return result
注释版:

"""先拆分, 后归并, 拆分: 递归调用merge_sort(), 将整个列表拆分成n个小列表, 小列表的长度为1 归并: 当列表拆分完毕之后, 执行下面的代码, 先进行比较然后进行归位, 然后返回函数的引用 """ import random def merge_sort(Li): # 先判断传递进来的列表的长度, 如果列表的长度小于等于1, 直接返回 # 列表的长度小于等于1, 分两种情况 # 1. 起始传递进来的就是一个空列表或列表只有一个元素, 那么将他返回 # 2. 在merge_sort()函数体内, 将起始的列表进行拆分, 被拆分之后的小列表, 如果长度为一, 则不能再进行拆分, 将小列表返回 n = len(Li) if n <= 1: return Li mid = n // 2 # 1. 设置列表的中间下标, 将原来的列表进行切片, 产生两个新的列表: 左列表, 右列表. # 2. 分别对这两个列表, 执行merge_sort()函数 # 3. 其实merge_sort()函数, 是先对列表进行拆分, 拆分完毕之后, 再将挨着的两个列表进行合并 left_Li = merge_sort(Li[:mid]) right_li = merge_sort(Li[mid:]) left_pointer, right_pointer = 0, 0 # 设置两个指针, 分别指向两个列表 result = [] # 设置一个空列表, 将比对之后的元素, 追加到这个列表内 while left_pointer < len(left_Li) and right_pointer < len(right_li): # 遍历两个列表, 如果其中一个列表遍历完毕, 则终止循环 if left_Li[left_pointer] <= right_li[right_pointer]: # 如果左列表的元素, 小于等于右列表的元素, 将元素追加到新列表内 # 指针向后移动 result.append(left_Li[left_pointer]) left_pointer += 1 else: # 如果左列表的元素, 大于右列表的元素, 将右列表的元素追加到新列表内 # 指针向后移动 result.append(right_li[right_pointer]) right_pointer += 1 # 上面循环结束后, 代表其中一个列表遍历完毕, 将另外列表的内的元素追加到新列表内 # 然后将新列表返回 result += left_Li[left_pointer:] result += right_li[right_pointer:] return result # 因为这个函数是递归调用[自己调用自己], 当递归到底的时候, 执行合并, 合并完毕, 返回调用, 然后再次执行合并 if __name__ == "__main__": l = list(i for i in range(0, 10000 )) print("洗牌之前的列表:" + str(l)) random.shuffle(l) print("洗牌之后的列表:" + str(l)) print(merge_sort(l))
注意:
归并排序相较于其他排序来说,
归并排序时产生了新的列表, 消耗内存, 效率降低
其他列表只是在原列表的基础上进行操作的
