一、堆排序概述
当你看到这里请去原作者那里点个赞, 原文链接
1.堆是一种数据结构
可以将堆看作一棵完全二叉树,这棵二叉树满足,任何一个非叶节点的值都不大于(或不小于)其左右孩子节点的值。 
2. 堆的存储
一般用数组来表示堆,若根节点存在于序号0处,i结点的父结点下表就为(i-1)/2,i结点的左右子结点下标分别为2i+1和2i+2
3. 堆排序思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
4. 堆排序的实现
堆排序需要解决两个问题:
- 如何由一个无序序列建成一个堆
- 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
针对第二个问题:一般在输出堆顶元素之后,视为将这个元素排除,然后用表中最后一个元素填补它的位置,自上向下进行调整:首先将堆顶元素和它的左右子树的根结点进行比较,把最小的元素交换到堆顶;然后顺着被破坏的路径一路调整下去,直至叶子结点,就得到新的堆。
Step 1: 构造初始堆
初始化堆时是对所有的非叶子结点进行筛选
最后一个非终端元素的下标是[n/2]向下取整,所以筛选只需要从第[n/2]向下取整个元素开始,从后往前进行调整。
Step 2:进行堆排序
堆排序是一种选择排序。建立的初始堆为初始的无序区。
排序开始,首先输出堆顶元素(因为它是最值),将堆顶元素和最后一个元素交换,这样,第n个位置(即最后一个位置)作为有序区,前n-1个位置仍是无序区,对无序区进行调整,得到堆之后,再交换堆顶和最后一个元素,这样有序区长度变为2。。。
不断进行此操作,将剩下的元素重新调整为堆,然后输出堆顶元素到有序区。每次交换都导致无序区-1,有序区+1。不断重复此过程直到有序区长度增长为n-1,排序完成。
5. 堆排序实例
1)首先,建立初始的堆结构图 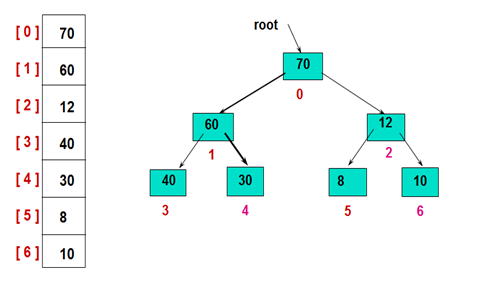
2)然后,交换堆顶的元素和最后一个元素,此时最后一个位置作为有序区(有序区显示为黄色),然后进行其他无序区的堆调整,重新得到大顶堆后,交换堆顶和倒数第二个元素的位置…… 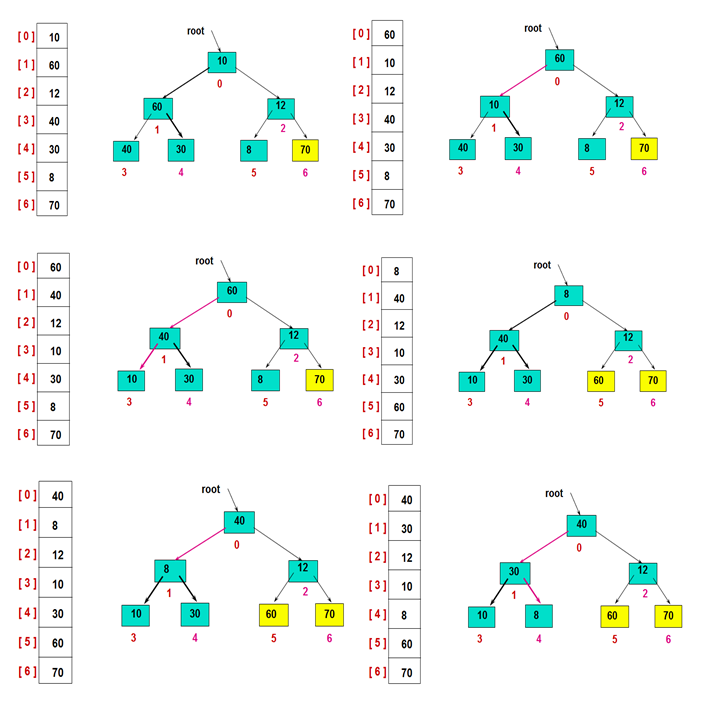
3)重复此过程 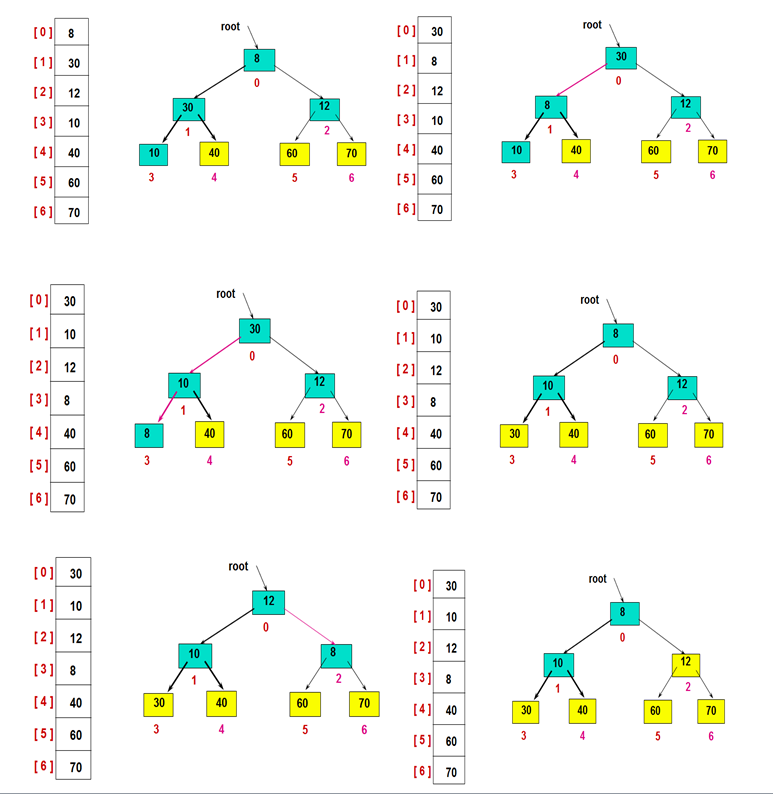
4)最后,有序区扩展完成即排序完成 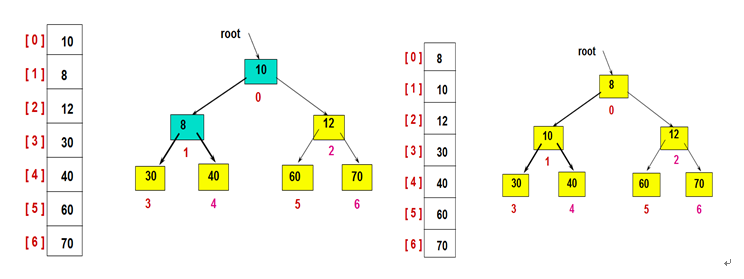
由排序过程可见,若想得到升序,则建立大顶堆,若想得到降序,则建立小顶堆。
6. 堆排序分析
稳定性:
时间复杂度:O(nlogn)
空间复杂度:
堆排序方法对记录数较少的文件并不值得提倡,但对n较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。
二: Python代码
简洁版:

def sift_down(arr, start, end): root = start while True: # 从root开始对最大堆调整 child = 2 * root + 1 if child > end: break # 找出两个child中交大的一个 if child + 1 <= end and arr[child] < arr[child + 1]: child += 1 if arr[root] < arr[child]: # 最大堆小于较大的child, 交换顺序 arr[root], arr[child] = arr[child], arr[root] # 正在调整的节点设置为root root = child else: # 无需调整的时候, 退出 break def heap_sort(arr): # 从最后一个有子节点的孩子来调整最大堆 first = len(arr) // 2 - 1 for start in range(first, -1, -1): sift_down(arr, start, len(arr) - 1) # 将最大的放到堆的最后一个, 堆-1, 继续调整排序 for end in range(len(arr) -1, 0, -1): arr[0], arr[end] = arr[end], arr[0] sift_down(arr, 0, end - 1)
注释版:

def sift_down(arr, start, end): root = start while True: # 从root开始对最大堆调整 child = 2 * root + 1 # child为root的左孩子 if child > end: # 超出序列的范围 break # 找出两个child中较大的一个 if child + 1 <= end and arr[child] < arr[child + 1]: # 如果右孩子存在, 而且左孩子小于右孩子 child += 1 # 将child指向右孩子 if arr[root] < arr[child]: # 如果root 小于 它的较大child arr[root], arr[child] = arr[child], arr[root] # root 与 child, 交换位置 root = child # 正在调整的节点设置为root else: # 无需调整的时候, 退出 break def heap_sort(arr): # 从最后一个有子节点的节点 来 调整最大堆 first = len(arr) // 2 - 1 # first: 最后一个有子节点的节点的下标 for start in range(first, -1, -1): sift_down(arr, start, len(arr) - 1) # 将堆内的首节点存储到有序区 for end in range(len(arr) -1, 0, -1): arr[0], arr[end] = arr[end], arr[0] sift_down(arr, 0, end - 1) """ 有序区: 从尾节点的位置, 根据循环的次数, 依次向前移动, 直到堆为空, 即: 有序区的长度为堆的原始长度 1. for end in range(len(arr)-1, 0, -1) len(arr)-1: arr内的最后一个节点的下标 end: 从arr的最后一个节点开始遍历, 即: 将arr倒序遍历 2. arr[0], arr[end] = arr[end], arr[0] 将arr内的首节点, 存储到有序区 1. arr[0]: root节点, 堆顶, arr内的第一个元素, 如果arr是大顶堆, 则是arr内的最大元素, 如果arr是小顶堆, 则是arr内的最小元素 2. arr[end]: arr内的尾节点, 有序区的首节点 根据循环的次数, 位置依次向前移动 """ if __name__ == "__main__": l = list(i for i in range(0, 1000)) print("洗牌之前的列表:" + str(l)) random.shuffle(l) print("洗牌之后的列表:" + str(l)) heap_sort(l) print(l)
