今天总结一下两种性能优秀的排序算法,归并排序与快速排序。
首先,二者都运用了递归和分治的两种重要思想。在这里递归就不做详细介绍。
分治:顾名思义,分而治之,这是在排序中我们非常常见的一种思想,同时也是在其他场景乃至日常生活的优秀解题方法。当我们遇到一个大的难题无从下手时,我们往往都会将其分成几个小块,当我们处理好每个小模块问题后,将其合并,大的问题便能够的以解决。同样,在我们处理排序问题时,也能充分利用分治思想来提高性能。
那么我们先来总结归并排序
归并排序(自顶向下,之后有简单的自底向上讲解)
归并排序的思想其实很简单,总共分为两步,分与治。
当我们面对一个很大的数组时,用以往学过的冒泡,插入,选择排序总是有些过于缓慢,希尔排序虽然可以,但是也不是最好的选择,因为它时间花费是平方级别的。如果我们内存中有足够大的空间,我们不妨使用提高空间复杂度来换取减少时间复杂度的思想,这样便能更快完成排序。
归并排序时,我们先将要进行排序的数组分为两部分,我们叫做Left和Right,如果我们先将这两部分都进行排序完成后,即子数组Left和Right都是有序数组。那么我们将这两个数组进行合并。
下面是具体思路:首先创建一个与原数组容量相同的数组用来存放合并时的数据,然后比较Left和Right中的数组,如果Left[0]<Right[0],将Left[0]放入新数组的0索引处,然后比较Left[1]和Right[0],依次类推按照升序或降序的方式便能将Left和Right中所有数组按照一定顺序拷贝进入新数组,此时就完成了数组排序。
那么我们又该如何对Left和Right数组进行排序呢?实际上,归并排序的模型中并不是将一个数组只分为两块,而是分为数组最小单元,length = 1,再对每个最小单元进行治的处理,这种处理方式要通过递归思想来进行实现。
下面让我们结合图片来进行详细的解释。
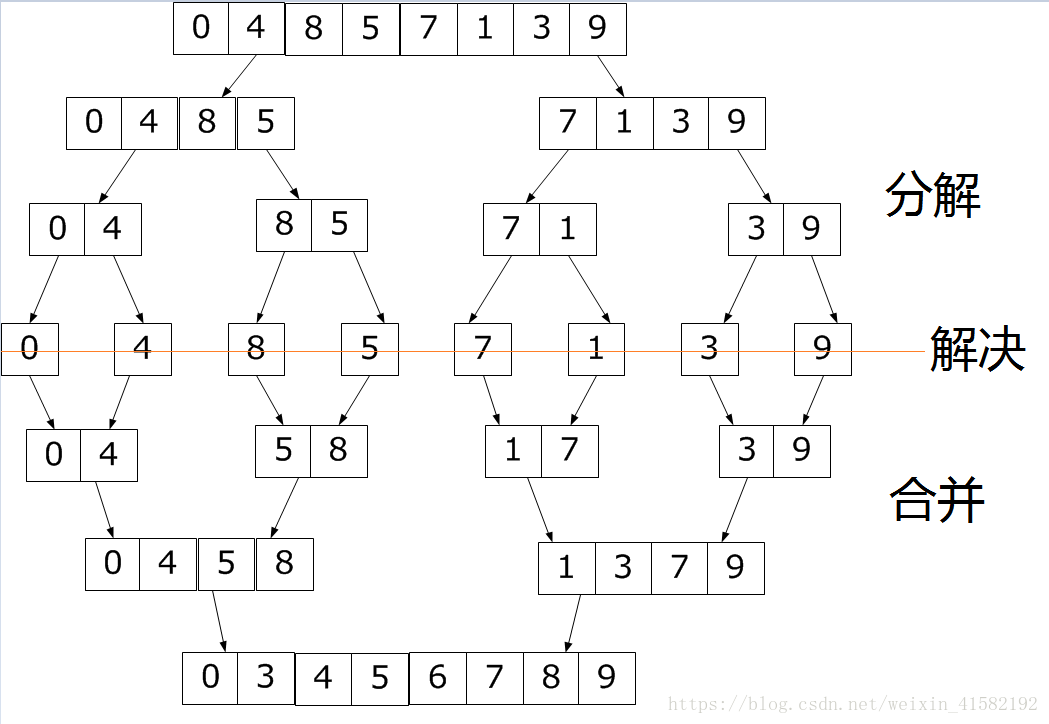
我们可以看到,归并排序将一个数组进行有限次的分割,再进行相同次数的合并,将整个数组进行排序,在我们使用递归实现归并排序时,并不需要过多的关注每一步都是如何进行操作,只需要将大体的思路分析清楚即可进行操作。
下面来看一段代码。
package SORT;
public class MergeSort {
public static void mergeSort(int[] arr) {
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
}
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
//参数分别为 待排序数组,左指针,有指针,辅助数组
//因为使用了递归,所以我们必须规定递归条件否则将进行无线循环
while (left < right) {
//将数组进行分割
int mid = (left + right) / 2;
//对左子数组继续进行归并排序
mergeSort(arr, left, mid, temp);
//对右子数组继续进行归并排序
mergeSort(arr, mid + 1, right, temp);
//将数组进行合并
Merge(arr, left, mid, right, temp);
}
}
//合并函数
public static void Merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
//t为辅助数组的索引
int t = 0;
while (i <= mid && j <= right) {
//当二者都没有到达最后一位时,进行比较并向辅助数组复制
if (arr[i] < arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
//当其中一个数组复制完毕后,将另一个数组内的数组全部复制进辅助数组
while (i <= mid) {
temp[t++] = arr[i++];
}
while (j <= right) {
temp[t++] = arr[j++];
}
t = 0;
//将辅助数组内已经排好的数据全部复制进原数组,排序完成
while (left <= right) {
arr[left++] = temp[t++];
}
}
}
在注释中很详细的分析了代码各个步骤的意义和实现方法。下面主要说下归并排序的一些其他特点。
对小规模的数组使用插入排序
我们知道,插入排序适合小规模和数组内数据具有一定顺序的情况。当我们使用归并排序时,在数组规模很小时依旧要进行分治处理,这样可能会因为过于频繁的递归调用函数,造成一定的性能损失(当然对于总体来说,这个损失并非不可承受),那么我们可以考虑一种更加折中的办法,我们来设置一个阀值,当我们将数组分给到以这个阀值为容量的子数组时,我们就不再进行递归处理,来使用更加快捷的插入排序,这样能够提升一定的性能,当然这个阀值的设置并没有明确指出,需要我们进行多次测试。这算是对归并排序的一个小小补充,根据一些资料测试,能够提升大约百分之二十左右的性能。
下面我们总结自底向上的归并排序
接下来我们简单谈一下,自底向上的归并排序。这种思想主要是先归并那些微型数组,然后再成对归并所得到的子数组,直到我们将整个数组进行完全的排序。实现这种归并的方式代码将更加简洁。
首先我们进行两两归并(把每个元素都当作大小为1的数组),然后四四归并(将大小为2的数组归并为大小为4的数组),通过这种方式,最后归并的两个数组可能大小不等,但和依旧为原数组。这种方式是从数据一端开始进行归并,而非自顶向下中从两端进行归并。
那么这两种方式区别又再哪里呢?当数组长度为2的N次幂时,这两种方式对数组的访问是相同的,对于时间消耗也是相同的。其他时候,这两种对数组访问次数和次序有所不同。
自底向上的归并排序比较适合用链表组织数据,当我们按照大小为1的子链表进行排序,然后是大小为2,大小为4.我们只需要重新将链表连接就能进行原地排序。不需要开辟额外空间。
关于希尔排序和递归排序速度一直是一个具有争议的问题,《算法》第四版中指出,在实际应用中,二者运行时间之间的差距在常数级别之内(希尔排序使用为经验证的递增序列),因此性能取决于具体实现。理论上来说,还没有人能够证明希尔排序对于随机数据的运行时间是线性对数接别的,因此存在平均情况下希尔排序的性能增长率更高的可能性,而在最坏情况下,这种差距的存在已经被证明了,但对于实际使用没有影响。
快速排序
快速排序作为应用最广泛的排序算法,流行的原因主要因为实现简单。快排具有非常大的优势在于两方面。
快速排序是原地排序(只需要非常小的一个辅助栈)
快速排序时间消耗,长度为N的数组排序时间与NlgN成正比
目前大多数排序算法都不能将这两点结合实现。而且快速排序的内循环比大多数排序的内循环要简洁许多,这样无论从理论上还是实际使用上都会更快。但是快速排序主要的缺点已经非常明显,快速排序非常脆弱,使用时要非常小心才能避免性能变的低劣。很多例子表明快速排序因为一些错误使时间的消耗成为平方级。
下面来看下快速排序的定义。
快速排序同样是一种分治思想的排序方法。它将一个数组分为连个数组,将两部分独立排序。快速排序和归并排序是互补的:归并排序将数组分成两个子数组分别排序,并将有序的子数组归并后整个排序,而快速排序将数组排序的方式则是当两个自数据都有序是整个数组也就自然有序了。这段定义出自于《算法》第四版,相信看起来会有些迷茫。下面我用自己总结的话来描述下快速排序的实现方法。
当我们面对一个要排序的数组时,我们首先要找一个基准数(这个基准数没有特殊限定,一般去数组第一个数),然后我们想办法将数组中大于这个基准数的数据放在基准数的一端,小于基准数的数据放在另一端。现在我们就得到了两个子数组,虽然这两个子数组并不是排序完成的,但我们能确定,其中一个子数组内所有的数都小于另一个,也就是说,当我们将这两个子数组排序完成时,整个数组自然就有序了。那么现在就是使用分治思想的地方,分开这两个数组后,再利用上述思想,同样找基准数,将数据按基准数分开两边,这时,我们就拥有了四个子数组。以此下去,当我们每个子数组都是有序的,那么我们就排序完成了。通过递归我们可以实现这一步骤。
以上过程由图片表示就是
那么我们如何经过代码实现呢?
首先我们需要在数组两端分别设置两个引用(指针),左指针任务是向右扫描数组,当扫描到大于基准数(按照升序)的数据后停下,右指针向左扫描,每当找到小于基准数的数据时停下。当二者都停下时,交换现在二者指向的数据。最后将基准数和分界处数据的交换,整个过程就完成了,这时,数组就由基准数一分为二。
下面我们来看代码实现
package SORT;
public class QuickSort {
public static void quickSort(int[] arr) {
// 对函数进行封装
quickSor(arr, 0, arr.length - 1);
}
public static void quickSor(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int i = left;// 左哨兵
int j = right;// 右哨兵
int index = arr[i];// 基准数
int t = 0;
while (i < j) {
//当右侧数据大于基准数时,右指针向左扫描
while (arr[j] > index) {
j--;
}
//当左侧数据小于基准数时,左指针右左扫描
while (arr[i] < index) {
i++;
}
//当二者都停下时,交换数据
if (i < j) {
t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
//当整个过程完成时,将基准数和分界处的数据互换
arr[left] = arr[i];
arr[i] = index;
//递归处理
quickSor(arr, left, i - 1);
quickSor(arr, i + 1, right);
}
}
}
下面我们来总结下快速排序需要注意的几个重点
防止越界
当我们要处理数组中最大活着最小的元素时,一定要注意指针的计算方法,在这里非常容易发成数组下标越界的异常。
终止递归
因为快速排序使用了递归处理,所以需要设置终止循环条件,忘记设置编译器会报错,但是如果设置错误,没有注意细节,非常可能造成程序陷入死循环,而我们在处理死循环时首先想到的总是内循环代码,想要再次发现问题有很大困难,这就要求我们在设计程序时,优先将递归终止循环条件设计好。
下面来看下快速排序的算法改进问题
当我们要将快排多次执行或者放置在一个大型的库函数上时,我们应该更多考虑快排的性能优化,优秀的优化方案能对性能有很大帮助。
切换到插入排序
这是我们之前就提到的一个思想,当我们对小数组进行操作时,插入排序可能要比递归归并速度有所提高(《算法》中指出在5-15大小数组时,性能更优秀),所有可以对小数组进行插入排序,实现起来也非常简单
if (left + M >= right) {
//插入排序代码,具体操作不进行实现
sort(arr,left,right);
return;
}
只需要将跳出递归的语句进行改变。M值即为数组大小参数。原理为,当我们扫描到一定长度后,左指针和右指针差距就是M,这是就不进行递归处理了,进行插入排序后直接跳出循环。
熵最优的排序
在实际应用中,我们可能出现一个数组中有大量重复数据,例如人员生日等。在这种情况下,我们使用快速排序性能尚可,但对此有巨大的改进空间,具有将线性对数级改为线性级的潜能。当一个数组内具有很多相同数据时,进行分割后很有可能子数组内的数据都完全一样,这样的数组我们可以不需要排序,但是因为递归的使用,程序依旧会将其按照归并分割,这样势必将会造成资源的大量浪费。
这种优化方法叫做三向切分法快速排序,具体实现就不在这里进行展示,有时间单开出一个文章来详细总结一下。
---------------------
作者:问巷
来源:CSDN
原文:https://blog.csdn.net/weixin_41582192/article/details/81239266
版权声明:本文为博主原创文章,转载请附上博文链接!