写在前面:下面的内容都是论文中和自己理解的内容,如有错误还望告知,改正,谢谢。
之前说的都是利用分类思想来解决目标检测问题,今天要说的是用回归思想来解决目标检测问题的鼻祖,YOLO。
如果手洗干净的话,那我就上菜喽。
第一道菜:如何将目标检测用回归的思想来进行解决呢?
大家还记得回归说的是什么么?就拿最简单的线性回归来讲,是不是用一条直线来拟合数据,损失函数的设计用的是sum-squared error,对吧。YOLO设计的损失函数也是使用的这种形式。先拿出来吓唬吓唬你们,哼。
$loss$ =$ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(x_{i}-hat{x}_{i})^{2}+(y_{i}-hat{y}_{i})^{2}]$ + $ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(sqrt{w_{i}}-sqrt{hat{w}_{i}})^{2}+(sqrt{h_{i}}-sqrt{hat{h}_{i}})^{2}]$ + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}(C_{i}-hat{C}_{i})^{2}$ + $lambda_{noobj}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{noobj}(C_{i}-hat{C}_{i})^{2}$ + $sum_{i=0}^{S^{2}}1_{t}^{obj}sum_{{c}in{classes}}(p_{t}(c)-hat{p}(c))^{2}$
怎么样,看到每一项的最外面都是平方项了么。我感觉这就和线性回归是一样的,线性回归使用的模型是线性模型,损失函数是平方损失函数,这里使用的是神经网络中的模型(具体怎么搞接下来再说),使用的函数也是平方损失(至于哪些权重什么的暂时先忽略掉吧),因此才会说YOLO是用回归的思想解决目标检测问题。
第二道菜:YOLO是如何来设计网络的呢?(摘录自原文)
YOLO设计的网络的目标是:输入一整张的图片(暂时先不考虑图片大小的问题),然后利用整张图片的feature来预测每一个bbox,同时预测每个bbox的类别,因此才说YOLO能够一次的定位图片中的多个物体,先不考虑准确性,单是这一end-to-end的方式就已经很吸引人了,当然准确性也是很棒的,这就是为什么YOLO很吸引人的地方。
具体来说呢,就是将整幅图片划分为S*S个块(cells),图像中的每个物体的中心点一定会落在某一个块内(如果落在划分块的边缘上,随便指定一个就行了,不过一定要一致),然后这个块就来负责这个物体的预测。
设计方面,每一个块要预测B个bbox以及它们B个bbox的confidence scores,这些得分是用来反映这个cell包含物体的的置信度(白话就是是否包含物体),以及如果包含物体的话如何和Ground-Truth衡量,因此这个confidence socres的公式 表示就是$Probability(Objece) * IoU^{with}_{ground truth}$。如果cell中包含物体则为1,否则为0,至于IoU,那就进行IoU的计算呗。
其实这里就是将这个目标检测任务进行了一个划分,由于是多个物体检测,因此这种划分带来的好处就是使用同一种方法,可以解决多个问题。这里想想RCNN系列方法,使用的是完全不同的思路,我先随便(就这里理解吧)在图片上进行画框框,然后把这个框框送给网络进行判断是否是那个物体,这种方法的弊端就是要产生好多的框框,从之前的文中也可以看的出来,不说RCNN系列了,回到正文吧。
上面说的是宏观上的东西,下面来将上面的内容丰满一下。
其中每一个cell预测B个bbox,每个bbox要预测5个值。原文如下:Each bounding box consists of 5 predictions: x, y, w, h, and confidence.The (x; y) coordinates represent the center of the box relative to the bounds of the grid cell. The width and height are predicted relative to the whole image.这里我不太确定bounds of the grid cell怎么描述,应该源码里面有吧,对于宽和高进行了归一化。
每一个cell同时预测在有物体的条件下是那个类别的概率,即$Pro(Class|Object)$,不过虽然有B个bbox,每个cell仅仅预测一个其中一个bbox的概率情况,至于为什么这样,我还没想通,以后想明白了在修改过来。
好了,抽象的描述就到这里了,接下来要具体到网络了。
第三道菜:网络设计和训练
网络有24个卷基层和两个全连接层(最最最最重要的层,当然前面提取特征的层也和重要啦),网络的整体架构借鉴了GoogleNet的思想(当时是15年,最好的分类模型应该就是它了吧),下面放上一张整体结构的网络图表示敬意。
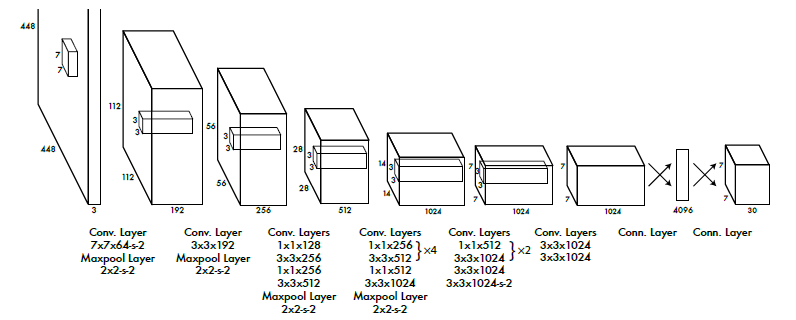
网络最后的输出是7 * 7 * 30的tensor,这些数据是怎么来的呢?这里要好好分析一下
7*7是因为论文中设置的S为7,30是因为论文中设置了2个bbox,因此需要10,对应的数据集上的20分类,因此才会有了最后的结果,其实从这里看网络模型本身并不复杂,其中最复杂的部分是想清楚这里面的东西。
网络的训练是也是采用了迁移学习的思想,在大的数据集上进行训练然后在在specific-tasks上进行fine-tune。首先在imagenet上进行训练前20个卷基层,然后有论文中提到增加卷积和池化可以提高性能,因此作者在后面有增加了4个卷积层和最后的2个全连接层,最后6层的初始化采用的是随机初始化的方式。在进行指定数据集上微调的时候,输入图像尺寸为448*448。整个网络模型使用的激活函数是rectified linear activation。到这里为止网络也设计好了,最后剩下的就是损失函数的设计了,要回到刚开始那一坨长长的公式了。
$loss$ =$ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(x_{i}-hat{x}_{i})^{2}+(y_{i}-hat{y}_{i})^{2}]$ + $ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(sqrt{w_{i}}-sqrt{hat{w}_{i}})^{2}+(sqrt{h_{i}}-sqrt{hat{h}_{i}})^{2}]$ + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}(C_{i}-hat{C}_{i})^{2}$ + $lambda_{noobj}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{npobj}(C_{i}-hat{C}_{i})^{2}$ + $sum_{i=0}^{S^{2}}1_{t}^{obj}sum_{{c}in{classes}}(p_{t}(c)-hat{p}(c))^{2}$
由于是回归问题,因此作者整体上选择的损失函数是sum-squared error,那么需要优化的有哪几部分信息呢?整个模型是要预测bbox以及类别的,因此bbox的预测算是要优化的一部分信息,再有就是确定了bbox之后如何评估这个bbox算是一部分,还有就是类别的判断算作是一部分。
因此模型的损失函数应该是这样的:
$loss$ =$sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(x_{i}-hat{x}_{i})^{2}+(y_{i}-hat{y}_{i})^{2}]$ + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(sqrt{w_{i}}-sqrt{hat{w}_{i}})^{2}+(sqrt{h_{i}}-sqrt{hat{h}_{i}})^{2}]$(这两部分是评估bbox) + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}(C_{i}-hat{C}_{i})^{2}$(评估confidence) + $sum_{i=0}^{S^{2}}1_{t}^{obj}sum_{{c}in{classes}}(p_{t}(c)-hat{p}(c))^{2}$(评估类别),完美。为啥子和论文中的公式不一样?没关系,下面会一步一步的改进的。
首先定位错误的权重和分类错误的权重是不一样的。如果定位都不正确,怎么来谈分类的正确,分类是在定位之后的事情(话是这样说但是这可以同时实现,YOLO就这这么做的),就算是RCNN系列也是这么做的,因此在前两部分增加了一个超参数$ lambda_{coord}$,而最后一部分没有增加超参数。因此公式就变成了这样子:
$loss$ =$ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(x_{i}-hat{x}_{i})^{2}+(y_{i}-hat{y}_{i})^{2}]$ + $ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(sqrt{w_{i}}-sqrt{hat{w}_{i}})^{2}+(sqrt{h_{i}}-sqrt{hat{h}_{i}})^{2}]$ + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}(C_{i}-hat{C}_{i})^{2}$ + $sum_{i=0}^{S^{2}}1_{t}^{obj}sum_{{c}in{classes}}(p_{t}(c)-hat{p}(c))^{2}$
不对吧,怎么和论文中的公式相比少了一项,这就给出缘由。原文如下:in every image many grid cells do not contain any object. This pushes the “confidence” scores of those cells towards zero, often overpowering the gradient from cells that do contain objects. This can lead to model instability, causing training to diverge early on.
这句话的意思是说,对于一副图片来讲,按照论文中的方式进行操作,有很多的cells中是没有物体的,因此如果对所有的cells赋予相同的权重(上式),可能会造成模型的不稳定,因此将上面的第二部分拆分为了两部分,有物体的cells和没有物体的cells,同时对于没有物体的cells赋予较低的权重$lambda_{noobj}$,最后的式子就变成这样了。
$loss$ =$ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(x_{i}-hat{x}_{i})^{2}+(y_{i}-hat{y}_{i})^{2}]$ + $ lambda_{coord}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}[(sqrt{w_{i}}-sqrt{hat{w}_{i}})^{2}+(sqrt{h_{i}}-sqrt{hat{h}_{i}})^{2}]$ + $sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{obj}(C_{i}-hat{C}_{i})^{2}$ + $lambda_{noobj}sum_{i=0}^{S^2}sum_{j=0}^{B}1_{ij}^{noobj}(C_{i}-hat{C}_{i})^{2}$ + $sum_{i=0}^{S^{2}}1_{t}^{obj}sum_{{c}in{classes}}(p_{t}(c)-hat{p}(c))^{2}$
这下子和论文中的公式完全一致了吧!
这部分上面的内容仅仅是一小部分,有些细节论文中写的很详细,因此在这里就没有多说。
论文中对于$lambda_{coord}$和$lambda_{noobj}$赋予的权重分别是5和0.5,反正我是觉得后面的权重给大了,相比较而言没有物体的cells个数是很多的,但是这里给出的权重仅仅是有物体的$frac{1}{2}$。可能这些数据是在指定数据集上的测试的数据吧。
详细看公式会发现第一部分的第一项和第二项里面的形式是不同的,这是因为bbox(指的是长和宽)的权重和中心点的预测的权重应该是不同的。损失函数中中应该反映出,对于同样的偏差,小的bbox应该比大的bbox更重要。这又是为什么呢?画个图描述一下吧。
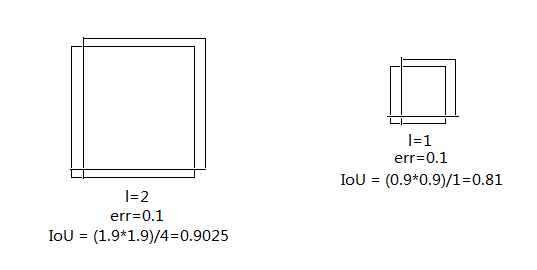
画的优点简陋,但是表达的意思应该可以理解吧。
为了解决这个问题,作者对于bbox的长和宽是要用的是square root error。我很好奇既然都是用了square root error,那为什么不直接使用log error?
到这里应该算做讲完YOLO了吧。
还有一道汤:messes in the model
这部分就比较混杂了,那就看这些吧。
对了,想说一句,模型的训练数据应该怎么处理呢?要是看到这这个还不明白,那就是没看懂哦,少年,你要加把劲了。
在测试的时候同样会产生2个bbox,毫无疑问是选择那个IoU较大的那个,因此这就指定了预测那个bbox中的物体。
为了防止过拟合,使用了dropout和数据增强,唉,最烦的就是这种细节,令人头疼,就没有不做数据增强,直接将图像扔到网络中目标识别算法么?
网络的最后使用了Non-maximal suppression,用来挑选出最合适的bbox
饭后小甜点:总结一下
上面虽然说了很多,都是一些很详细的事情,这些东西都是可以从论文中找到的。这里说一点自己的见解。YOLO网络模型采用回归的思想来解决目标检测问题,其中最重要的就是损失函数了,这倒不是说这个损失函数有多难,上面也进行了一些分析,最最主要的是将检测问题进行了一个划分,同时也将问题进行了一定程度的编码,也就是最后一层全连接层的设计,最后就是充分利用神经网络的逼近能力,简直就是恰到好处。我一直想知道他们这个实验做了多久,因为没做之前网络能不能收敛都不知道,况且论文中给出的调参步骤也是挺吓人的,这篇论文虽然看着简单,速度快效果好,人家实现起来可真不简单,这真的是一篇实至名归的文章。接下来准备看看源码以及YOLO-V2版本,就这样吧。
各位看官吃喝的怎么样啦,吃好再来哦,免费的呦。