ACM学习历程——HDU5017 Ellipsoid（模拟退火）（2014西安网赛K题）

---恢复内容开始---

Description

Given a 3-dimension ellipsoid(椭球面) 

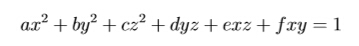
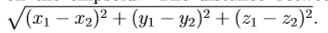
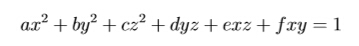
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x ₁,y ₁,z ₁) and (x ₂,y ₂,z ₂) is defined as 

 

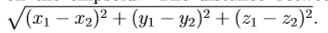
Input

There are multiple test cases. Please process till EOF. 

For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f (0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double. 

 

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10 ^-5.

 

Sample Input

1 0.04 0.01 0 0 0

 

Sample Output

1.0000000

 

 

这个题目可以模拟退火来做，可以在某一点朝八个方向搜索，如果使距离变小了，自然就朝那个方向走step步长，不过步长需要随次数按比率变小。当步长到达esp，自然精度达到了要求。不过需要注意的是要判断z根不存在的情况，以及两个根取距离最小的。几次测试后step的减小系数是0.97到0.99是可以过的。

 

代码：

 

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define esp 1e-7

using namespace std;

bool flag;
double a, b, c, d, e, f;

double getz(double x, double y)
{
    double A = c;
    double B = d*y + e*x;
    double C = f*x*y + a*x*x + b*y*y - 1.0;
    double v = B*B - 4*A*C;
    if (v < 0)
    {
        flag = 0;
        return 0;
    }
    flag = 1;
    v = sqrt(v);
    double z1 = (v-B) / A / 2.0;
    double z2 = (-v-B) / A / 2.0;
    if (fabs(z1) < fabs(z2))
        return z1;
    else
        return z2;
}

double dis(double x, double y)
{
    double z = getz(x, y);
    if (flag == 0)
        return 0;
    return sqrt(x*x + y*y + z*z);
}

double qt()//模拟退火
{
    double x = 0, y = 0, Min = dis(x, y);
    double xx, yy, len;
    double step = 1;
    while (step >= esp)
    {
        for (int dx = -1; dx <= 1; ++dx)
        {
            for (int dy = -1; dy <= 1; ++dy)
            {
                if (dx == 0 && dy == 0)
                    continue;
                xx = x + step*dx;
                yy = y + step*dy;
                len = dis(xx, yy);
                if (flag && len < Min)
                {
                    Min = len;
                    x = xx;
                    y = yy;
                }
            }
        }
        step *= 0.97;
    }
    return Min;
}

int main()
{
    //freopen("test.txt", "r", stdin);
    while (scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &e, &f) != EOF)
    {
        printf("%.7lf
", qt());
    }
    return 0;
}