ACM学习历程—HDU1028 Ignatius and the Princess（组合数学）

Ignatius and the Princess  

Description

       "Well, it seems the first problem is too easy. I will let you know how foolish you are later." feng5166 says.       
"The second problem is, given an positive integer N, we define an equation like this:          N=a[1]+a[2]+a[3]+...+a[m];          a[i]>0,1<=m<=N;        My question is how many different equations you can find for a given N.        For example, assume N is 4, we can find:          4 = 4;          4 = 3 + 1;          4 = 2 + 2;          4 = 2 + 1 + 1;          4 = 1 + 1 + 1 + 1;        so the result is 5 when N is 4. Note that "4 = 3 + 1" and "4 = 1 + 3" is the same in this problem. Now, you do it!"

Input

The input contains several test cases. Each test case contains a positive integer N(1<=N<=120) which is mentioned above. The input is terminated by the end of file. 

Output

For each test case, you have to output a line contains an integer P which indicate the different equations you have found.        

Sample Input

4

10

20 

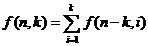
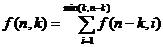
Sample Output

5

42

627

 

刚看到题目是k个数相加为n的题目，第一反应是求1到n元的一次不定方程求解，用插板的方法就能求出通项，但是考虑到这k元未知数是没有先后关系的，也就是说任意(a,a)和(a,a)是相同的。于是不能这样考虑。
然后考虑到每组解必然有个最大值，于是设了这样一个函数（或者数组）f(n,k)，表示和为n且最大数为k的上述元数不定的方程的解的个数。这样一来题目要求求得就是f(n,1)到f(n,n)的和了。
然后我们考虑，对于f(n,k)如果去掉最大值k，那么其子问题就是求和为n-k且最大值小于等于k的上述方程的解的个数。 于是得到递推方程：

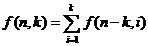
但是考虑到n-k或许会比k还要小，于是更新递推方程为：

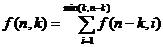
然后打表求f(n,k)即可，此外用f(n,0)来存所有f(n,i)的和。用数组实现。


代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <vector>
#define inf 0x3fffffff

using namespace std;

int a[125][125];

int main()
{
    //freopen ("test.txt", "r", stdin);
    memset (a, 0, sizeof(a));
    for (int i = 1; i <= 120; ++i)
    {
        for (int j = 1; j <= i; ++j)
        {
            if (i == 1 || i == j)
            {
                a[i][j] = 1;
            }
            else
            {
                for (int k = 1; k <= j && k <= i-j; ++k)
                {
                    a[i][j] += a[i-j][k];
                }
            }
            a[i][0] += a[i][j];
        }
    }
    int n;
    while(scanf("%d", &n) != EOF)
    {
        printf ("%d
", a[n][0]);
    }
    return 0;
}