描述
给你一个m x n (1 <= m, n <= 100)的矩阵A (0<=aij<=10000),要求在矩阵中选择一些数,要求每一行,每一列都至少选到了一个数,使得选出的数的和尽量的小。
输入
多组测试数据。首先是数据组数T
对于每组测试数据,第1行是两个正整数m, n,分别表示矩阵的行数和列数。
接下来的m行,每行n个整数,之间用一个空格分隔,表示矩阵A的元素。
输出
每组数据输出一行,表示选出的数的和的最小值。
数据范围
小数据:1 <= m, n <= 5
大数据:1 <= m, n <= 100
- 样例输入
-
2 3 3 1 2 3 3 1 2 2 3 1 5 5 1 2 3 4 5 5 1 2 3 4 4 5 1 2 3 3 4 5 1 2 2 3 4 5 1
- 样例输出
-
Case 1: 3 Case 2: 5
题目大意是有三类纪念品A、B、C。每类纪念品又有N种不同的纪念品Ai、Bi、Ci(1 <= i <= N),然后对于Ai纪念品的剩余个数CAi是N+1-i个,对于Bi纪念品的剩余个数CBi是N+1-i个,Ci纪念品的剩余个数CCi是N+1-i个。
要求拿出三件纪念品Ap, Bq, Ck,不能恰好有两件价值相同,求取法数。
可以从两个角度考虑:
(1) 从正面角度考虑:
不能恰好有两件价值相同,那么就是三件价值都相同或者都不同。
1. 三件价值都相同:
假设我都取价值为i的纪念品,那么就有CAi*CBi*CCi可以取(CAi、CBi、CCi分别为Ai、Bi、Ci剩余个数)
所以总数便是
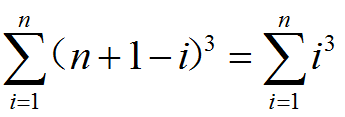
2.三件价值都不同:
假设我A取了价值为i的纪念品,那么有CAi种;
那么B不能取价值为i的,假设B取了价值为j的,有CBj种;
那么C不能取价值为i和j的。
所以总数便是
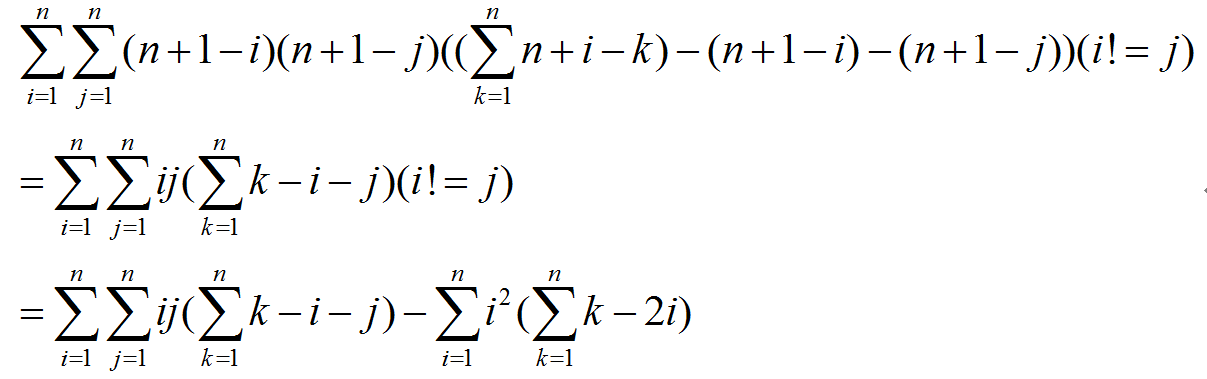
此处说明一下,第一个式子是取A乘取B乘取C(取C是在C总数的基础上减去价值为i和j的)
第二个式子就是第一个式子变形的,将n+1-i替换为i’,同理的j和k。
第三个式子就是把i != j这个条件体现出来。
接下来进一步化简:
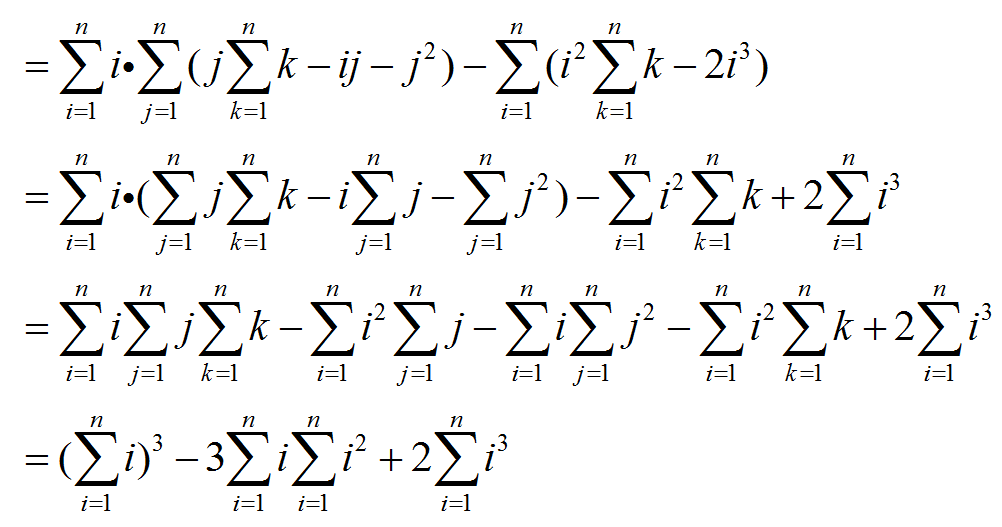
所以总的就是上面两种情况相加,得到
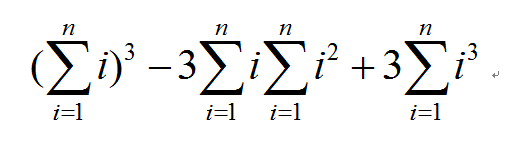
然后由下面三组式子便可以求解:
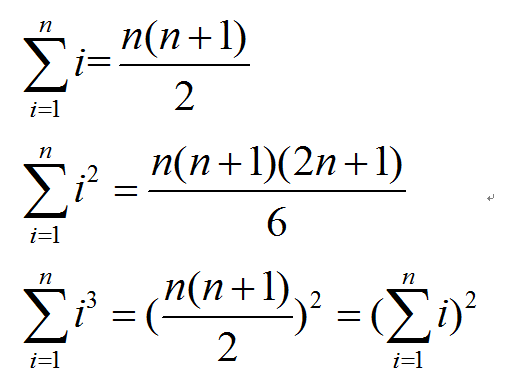
(2) 从反面角度考虑:
不能恰好有两件价值相同,那么就是总选数里面减去它就OK了。
总选数自然就是:
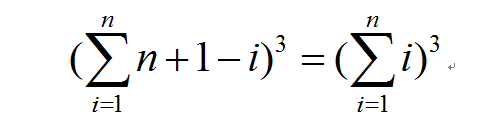
恰好有两件价值相同,那么就先从ABC三个里选出两种准备选价值相同的i,选法有C(2, 3),即3种。
然后剩余的一个不能选价值为i的,所以总数:

所以最后答案就是:
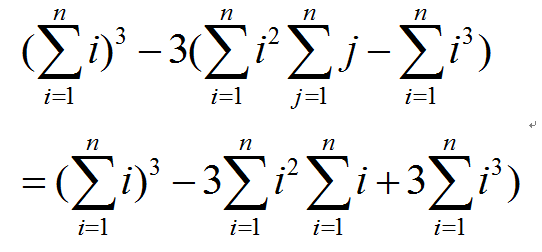
与第一种方法的答案一致。
代码:
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <cstring> #include <algorithm> #include <set> #include <map> #include <vector> #include <queue> #include <string> #define inf 0xfffffff #define eps 1e-10 #define N 1000000007 using namespace std; long long n, C1, C2; void Init() { n %= N; C1 = (n+1)*n/2; C1 %= N; C2 = (n+1)*n/2; if (C2%3 == 0) { C2 /= 3; C2 %= N; C2 *= 2*n+1; C2 %= N; } else { C2 %= N; C2 *= (2*n+1)/3; C2 %= N; } } long long ans() { long long s = (C1*C1) % N; s = (s*C1)%N + (3*s)%N - (3*((C1*C2)%N))%N; return (s%N+N)%N; } int main() { //freopen("test.txt", "r", stdin); int T; scanf("%d", &T); for (int times = 1; times <= T; ++times) { scanf("%lld", &n); printf("Case %d: ", times); Init(); printf("%lld ", ans()); } return 0; }