按道理来说,递归是很简单的。例如求斐波那契数的公式,
fibonaci(N) = fibonaci(N-1)+fibonaci(N-2)不复杂吧,再比方,阶乘公式:
Factorial(N) = N*Factorial(N-1)有啥难的呢?
但真正在面试、比赛或者工作中遇到的题目是这样的。
1、八皇后问题(面试):
在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问一共有多少种摆法。
2、递归遍历文件夹(工作)
3、打印一个数组的全排列(面试)
4、棋盘覆盖问题(竞赛)
那么,如何求解这些问题呢?
还是先从简单的解法入手引出递归。下面我们以八皇后来举例。其暴力求解方法如下:
def is_valid(position):
dim = len(position)
for i in range(dim):
for j in range(i+1,dim):
if position[i] == position[j]: #在同一列的情况
return False
if abs(position[i]-position[j]) == abs(i-j): #在同一个对角线的情况
return False
return True
def eight_queen():
solution_count = 0
for c1 in range(0,8):
for c2 in range(0,8):
for c3 in range(0,8):
for c4 in range(0,8):
for c5 in range(0,8):
for c6 in range(0,8):
for c7 in range(0,8):
for c8 in range(0,8):
if is_valid([c1,c2,c3,c4,c5,c6,c7,c8]):
solution_count+=1
else:
pass
return solution_count
print("八皇后解法总数:",eight_queen())def is_valid(position):最后程序输出解法总数为92。
这里有必要解释一下is_valid函数,该函数判断给定的8个棋子布局是否满足题目中的要求,也就是不能互相攻击。
大家需要注意的是,eight_queen()程序中,传递给is_valid函数的[c1,c2,c3,c4,c5,c6,c7,c8] 代表了第一行在第c1列放皇后,第二行在第c2列放皇后,第三行在第c3列放皇后,以此类推。
也就是说,这种摆法已经避免了出现2个皇后 在同一行的局面。
因此,is_valid函数主要判断这8个皇后的位置是否在同一列,或者同一条斜线上。
判断两个棋子是否在同一列比较简单,只需要判断position[i]是否等于position[j]即可。
那么,如何判断两个棋子是否在同一条斜线上呢?我们探索一些在同一斜线的情形:
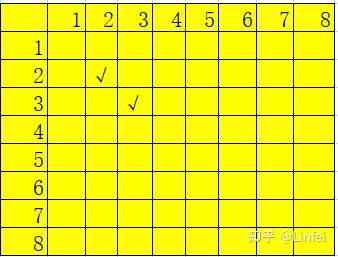
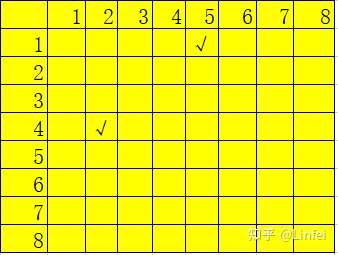
一共有两种情况,一种是向右下方的斜线,一种向右上方的斜线。
看看向右下方的斜线,
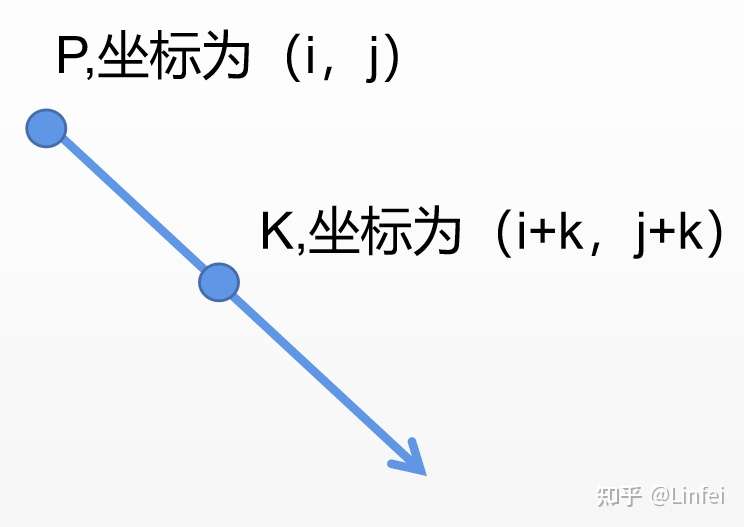
假设第一个皇后的位置是P,其坐标为(i,j),则向下倾斜时,该斜线上下一个位置的坐标是(i+1,j+1),第二个位置的坐标是(i+2,j+2),不失一般性,第n个位置的坐标是(i+N,j+N)
从上可知,点P和与其在一条斜线上的点K的坐标分别是(i,j),(i+k,j+k),下面尝试找到这两个位置的坐标有什么关联,也就是找这些几个整数的关联,我们从加减乘除的角度来考虑。
先试着把二者的坐标进行相加,得到:
x坐标相加得到结果X= i+i+k = 2*i + k
y坐标相加得到结果Y= j+j+k = 2*j + k
发现2个结果都有k,基于直觉,把二者相减,得到2*(j-i),猜测,是否Y-X是(j-i)的倍数,就说明二者在一条斜线上呢?很可惜猜错了,例如点(4,2)和(6,6),二者虽然不在一条斜线上,却有Y-X=2 ,是点(4,2)的y和x的差值的倍数。
看起来加法的尝试失败了。
减法呢?P和K这两点的X和Y坐标分别相减,得到
(i+k-i, j+k-j)= (k,k),就是说减法得到的结果,其X和Y值相等。
我们试了几个不在这条斜线上的点,发现这些点的值与P的x和y坐标相减,得到的X和Y确实不相等,因此,我们认推测如果某点Q(m,n)在(i,j)所在的向下斜线上,其x和y坐标值和点P的x,y坐标值相减后,m-i = n-j,即X和Y相等。
本结论实际上也很容易证明。
假设一个点Q在从P开始的从左到右向下倾斜的线上,其坐标表示为(i+k,j+k),由于这个斜线与Q所在的行只有Q一个交点(两条直线最多一个交点),只需要证明Q所在行的其他点不满足X=Y即可。
不失一般性,假设与Q在同一行的另一个点S的坐标是(i+k,j+m),这里m≠k(否则S和Q是同一个点),则S和P坐标相减后,X=i+k-i=k, Y=j+m-j=m,由于刚才的结论m≠k,得到X≠Y。
到这里,可以得到如下结果:
结论①:一个点K的坐标x和y分别减去P的坐标x和y,如果相等,则说明K在从P出发向右下方倾斜的斜线上。
下面研究向右上方倾斜的斜线。

我们发现K-P的结果是(k,-k),x和y坐标相反,大家也可以结合前面的分析,验证这个结论:
结论②:一个点K的坐标x和y分别减去P的坐标x和y,如果结果相反,则说明K在从P出发从左到右向上倾斜的斜线上。
汇总结论①和②,得到如下结论:
结论③:一个点K的坐标x和y分别减去P的坐标x和y,如果绝对值相等,则说明K在从P出发的斜线上。
注意:这里斜线的斜率都是±1(八皇后题目中限制了斜率为±1)
条件判断代码很好写,如下:
if abs(position[i]-position[j]) == abs(i-j): #在同一条斜线的情况
return False下面我们看下主流程代码:
solution_count = 0
for c1 in range(0,8):
for c2 in range(0,8):
for c3 in range(0,8):
for c4 in range(0,8):
for c5 in range(0,8):
for c6 in range(0,8):
for c7 in range(0,8):
for c8 in range(0,8):
if is_valid([c1,c2,c3,c4,c5,c6,c7,c8]):
solution_count+=1
else:
pass同样分析,这段代码很容易理解,但是扩展性上就很差了。如果问题改成100个皇后,就得改成100重循环,这可是很大的工作量,更主要的是,代码显得太丑陋了。
有什么解决办法呢?
我们这样分析,假设第一行已经放好了一个皇后(这个皇后放哪个列无所谓)。那么,剩下的七个皇后实际上也要满足“不能处于同一行、同一列或同一斜线上”的条件,也就是说假设我们有个eight_queen_2函数,实现了八皇后的解法,那么该函数同样也能够实现剩下的七皇后问题,就是说我们完全可以复用这个eight_queen2函数来完成剩下的七皇后问题,这也是递归的常见用法。
那么,这里的七皇后和八皇后的问题有什么联系呢?七皇后除了满足自身的七个皇后不在同一行、同一列或同一斜线上的条件外,唯一的联系就是这七个皇后不能和第一行的皇后在同一行、同一列或者统一斜线上。于是,我们得到的递归实现如下:
'''八皇后问题'''
occupied=[]
dim =8
solutions = 0
def is_valid(x,y,occupied):
global dim
for pos in occupied:
if pos[1] == y or abs(x-pos[0])==abs(y-pos[1]):
return False
return True
def sol_eight_queen(cur_row):
global occupied,solutions
if cur_row >= dim:
solutions+=1
return True
for j in range(dim):
if is_valid(cur_row,j,occupied):
occupied.append([cur_row,j])
sol_eight_queen(cur_row+1)
del occupied[-1]
def test_eight_queen():
sol_eight_queen(0)
print("total valid answers is:",solutions)运行test_eight_queen()函数,程序输出为92。
下面我们看看代码。判断布局是否符合要求的代码见is_valid程序,代码比较容易理解,这里不再详细介绍。
核心是sol_eight_queen(cur_row)程序。
其中,global eight_queen,occupied,dim,solutions定义了一些全局变量,用全局变量大多数时候不是很好的编程习惯,笔者这里为了简化代码编写采用了全局变量的方式。occupied保存了从第1行到当前行的王后摆放位置。solutions保存了可以成功摆放8个王后的布局数,也就是我们要求的结果。
if cur_row == dim:
solutions += 1
return True
这里是递归退出条件,可以理解成当摆放到棋盘的第9行时,认为前面已经成功拜访完毕前8行的王后。为此我们将solution加1。
for j in range(dim):
if is_valid(cur_row,j,occupied):
occupied.append([cur_row,j])
sol_eight_queen(cur_row+1)
del occupied[-1]这一段代码是核心逻辑。
for j in range(dim):
意味着我们对于当前行cur_row的每一列,执行下面的操作:
首先通过is_valid(cur_row,j,occupied)来判断在第cur_row行的第j列摆放王后,是否和之前摆放的王后冲突,如果冲突,则继续判断第j+1列;如果不冲突,则调用如下三行代码:
occupied.append([cur_row,j])
sol_eight_queen(cur_row+1)
del occupied[-1]通过occupied.append([cur_row,j])表明本行我们在(cur_row,j)位置摆放王后,然后递归调用sol_eight_queen(cur_row+1)进入下一行,也就是cur_row+1行;递归调用结束后,需要清理现场,也就是这里的del occupied[-1],即删除occupied数组中的最后一个元素。为什么呢?
如果不把[cur_row,j]这个位置的王后拿走,大家可以想象,后续放王后时相当于凭空多了这个不应该存在的限制条件,导致程序无解。大家可以自行删除del occupied[-1]后再运行,程序输出解的个数为0。
到这里,让我们暂停下,首先整理一下递归和循环的关系:
一、递归程序本身相当于1个循环,像这种:
factorial(n) = n*factorial(n-1)等价于:
result =1
for i in range(1,n+1):
result *= i二、2个递归调用,相当于顺序执行2个循环,例如:
factorial(n)+factorial(k)三、一个循环内部调用了递归,例如上述的八皇后问题,则相当于N重循环。再例如下面的文件夹遍历程序:
import os
def browser_dir(rootDir):
for lists in os.listdir(rootDir):
path = os.path.join(rootDir, lists)
if os.path.isfile(path):
print(path)
else:
browser_dir(path) 可以看出,循环内调用递归可以等价于多重循环的效果。大家自己写下代码好好体会下。
四、多重循环内部调用了递归,常见于图相关类型的题目,例如:
有一个H*W大小的游戏板,由黑白两种格子组成。现要用3个单位格子的L状板块把白色格子全部覆盖掉。板块可以自由旋转,但不能重叠覆盖黑色格子,或超出游戏版。
基本上能遇到的就是这些了,大家要铭记的是对于不同的题目,应用不同的循环+递归的策略。
建议大家好好体会下
for j in range(dim):
if is_valid(cur_row,j,occupied):
occupied.append([cur_row,j])
sol_eight_queen(cur_row+1)
del occupied[-1]这段代码,一个循环,一个进入下层递归的条件,同时注意恢复现场。
大多数问题要么需要你理清楚循环怎么写,要么理清楚进入下层递归的条件。最终,别忘了恢复现场。