http://acm.hdu.edu.cn/showproblem.php?pid=5120
Intersection
Time Limit: 4000/4000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others)Total Submission(s): 231 Accepted Submission(s): 101
Problem Description
Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.
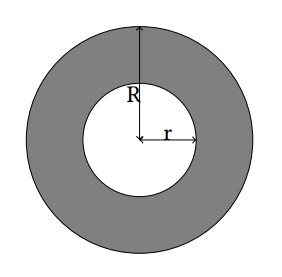
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.

Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.
Input
The first line contains only one integer T (T ≤ 105), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).
Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.
Each of the following two lines contains two integers xi, yi (0 ≤ xi, yi ≤ 20) indicating the coordinates of the center of each ring.
Output
For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.
Sample Input
2 2 3 0 0 0 0 2 3 0 0 5 0
Sample Output
Case #1: 15.707963 Case #2: 2.250778
Source
解题思路:代码中解释的很详细
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define pi acos(-1.0)
/*
已知:圆环心距,两圆环的内圆半径和外圆半径。
S = S(大圆1交大圆2) + S(小圆1交小圆2)- S(大圆1交小圆2) - S(小圆1交大圆2)
*/
struct P{
double x;
double y;
double r;
}p[4];;
//求两圆相交面积
double area(int i, double r1, int j, double r2){
double d = sqrt((p[i].x - p[j].x) * (p[i].x - p[j].x) + (p[i].y - p[j].y) * (p[i].y - p[j].y));//圆心距
if(r1 > r2){
double temp = r1;
r1 = r2;
r2 = temp;
}//r1取小
if(r1 + r2 <= d)
return 0;//相离
else if(r2 - r1 >= d)
return pi * r1 * r1;//内含
else {
double a1 = acos((r1 * r1 + d * d - r2 * r2) / (2.0 * r1 * d));
double a2 = acos((r2 * r2 + d * d - r1 * r1) / (2.0 * r2 * d));
return (a1 * r1 * r1 + a2 * r2 * r2 - r1 * d * sin(a1));
}//相交
}
int main(){
int t;
double r1, r2;
double x1, y1, x2, y2;
double s1, s2, s3, s4;
double ans;
int Case = 1;
scanf("%d", &t);
while(t--){
scanf("%lf %lf", &r1, &r2);
scanf("%lf %lf", &x1, &y1);
scanf("%lf %lf", &x2, &y2);
//小圆1
p[0].x = x1, p[0].y = y1, p[0].r = r1;
//大圆1
p[1].x = x1, p[1].y = y1, p[1].r = r2;
//小圆2
p[2].x = x2, p[2].y = y2, p[2].r = r1;
//大圆2
p[3].x = x2, p[3].y = y2, p[3].r = r2;
//大1小2
s1 = area(1, r2, 2, r1);
//小1大2
s2 = area(0, r1, 3, r2);
//大1大2
s3 = area(1, r2, 3, r2);
//小1小2
s4 = area(0, r1, 2, r1);
ans = s3 + s4 - s1 - s2;
printf("Case #%d: %.6lf ", Case++, ans);
}
return 0;
#include <stdlib.h>
#include <math.h>
#define pi acos(-1.0)
/*
已知:圆环心距,两圆环的内圆半径和外圆半径。
S = S(大圆1交大圆2) + S(小圆1交小圆2)- S(大圆1交小圆2) - S(小圆1交大圆2)
*/
struct P{
double x;
double y;
double r;
}p[4];;
//求两圆相交面积
double area(int i, double r1, int j, double r2){
double d = sqrt((p[i].x - p[j].x) * (p[i].x - p[j].x) + (p[i].y - p[j].y) * (p[i].y - p[j].y));//圆心距
if(r1 > r2){
double temp = r1;
r1 = r2;
r2 = temp;
}//r1取小
if(r1 + r2 <= d)
return 0;//相离
else if(r2 - r1 >= d)
return pi * r1 * r1;//内含
else {
double a1 = acos((r1 * r1 + d * d - r2 * r2) / (2.0 * r1 * d));
double a2 = acos((r2 * r2 + d * d - r1 * r1) / (2.0 * r2 * d));
return (a1 * r1 * r1 + a2 * r2 * r2 - r1 * d * sin(a1));
}//相交
}
int main(){
int t;
double r1, r2;
double x1, y1, x2, y2;
double s1, s2, s3, s4;
double ans;
int Case = 1;
scanf("%d", &t);
while(t--){
scanf("%lf %lf", &r1, &r2);
scanf("%lf %lf", &x1, &y1);
scanf("%lf %lf", &x2, &y2);
//小圆1
p[0].x = x1, p[0].y = y1, p[0].r = r1;
//大圆1
p[1].x = x1, p[1].y = y1, p[1].r = r2;
//小圆2
p[2].x = x2, p[2].y = y2, p[2].r = r1;
//大圆2
p[3].x = x2, p[3].y = y2, p[3].r = r2;
//大1小2
s1 = area(1, r2, 2, r1);
//小1大2
s2 = area(0, r1, 3, r2);
//大1大2
s3 = area(1, r2, 3, r2);
//小1小2
s4 = area(0, r1, 2, r1);
ans = s3 + s4 - s1 - s2;
printf("Case #%d: %.6lf ", Case++, ans);
}
return 0;
}