-
排序逻辑
构建大顶堆,将第一个元素和最后一个元素交换,然后在除去最后一个数的队列中构建大顶堆,然后再交换,直到大顶堆没有元素
排序之前必须直到二叉树的性质
长度为 n 的二叉树最后一个父亲节点为:n/2
第n个节点的左子节点:2n
第n个节点的右子节点:2n + 1
-
初始数据
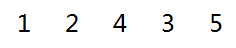
-
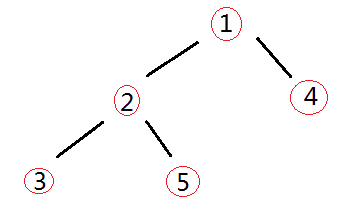
调整为大顶堆

-
交换
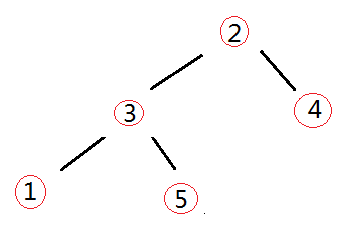
-
再次构建大顶堆
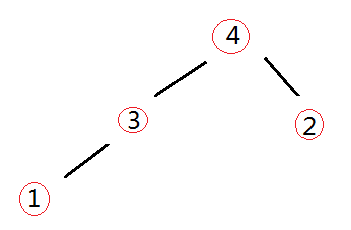
-
交换
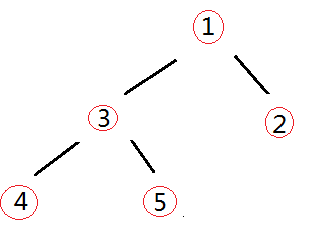
-
构建大顶堆
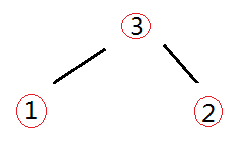
-
交换
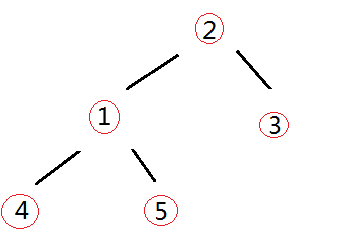
-
构建大顶堆
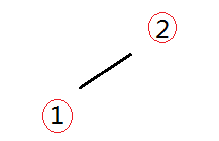
-
交换
-
-
代码示例
/** * * @param arr 因为大顶堆索引从1开始,所以传入的数组第0 个位置为(-1)充当占位符 * @param n 数组长度-1 */ public static void heapSort(int[] arr, int n){ int i; //构建大顶堆,n/2选中的是最后一个双亲节点 for(i=n/2; i>0; i--){ headAdjust(arr,i,n); } for(i=n;i>1;i--){ //大顶堆构建完成后交换第一个和最后一个元素的位置 swap(arr,1,i); //再在第一个和倒数第二个之间构建大顶堆 headAdjust(arr,1,i-1); } } /** * 构建大顶堆的方法 * @param arr 排序数组 * @param a 大顶堆的顶节点 * @param n 最后一个节点 */ public static void headAdjust(int[] arr, int a, int n){ int i,temp; // temp存储双亲节点的值 temp = arr[a]; //2*n指向左子节点 for(i=2*a;i<=n;i*=2){ //i指向左右子节点的最大节点 if(i<n && arr[i]<arr[i+1]){ i++; } //如果双亲节点的值大于子节点,退出循环 if(temp>arr[i]){ break; } arr[a] = arr[i]; a = i; count++; } arr[a] = temp; } public static void swap(int[] arr, int a, int b){ int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; } -
时间复杂度
O(nlogn)