原文链接:https://developers.google.com/machine-learning/crash-course/regularization-for-simplicity
正则化指的是降低模型的复杂度以减少过拟合。
1- L₂正则化
泛化曲线:显示的是训练集和验证集相对于训练迭代次数的损失。
如果说某个模型的泛化曲线显示:训练损失逐渐减少,但验证损失最终增加。那么就可以说,该模型与训练集中的数据过拟合。
根据奥卡姆剃刀定律,或许可以通过降低复杂模型的复杂度来防止过拟合,这种原则称为正则化。

也就是说,并非只是以最小化损失(经验风险最小化)为目标:

而是以最小化损失和复杂度为目标,这称为结构风险最小化:
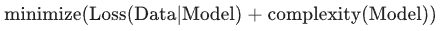
此时,训练优化算法是一个由两项内容组成的函数:一个是损失项,用于衡量模型与数据的拟合度,另一个是正则化项,用于衡量模型复杂度。
衡量模型复杂度的两种常见方式(这两种方式有些相关):
- 将模型复杂度作为模型中所有特征的权重的函数。
- 将模型复杂度作为具有非零权重的特征总数的函数。
如果模型复杂度是权重的函数,则特征权重的绝对值越高,对模型复杂度的贡献就越大。
可以使用 L2 正则化公式来量化复杂度,该公式将正则化项定义为所有特征权重的平方和:

在这个公式中,接近于 0 的权重对模型复杂度几乎没有影响,而离群值权重则可能会产生巨大的影响。
例如,某个线性模型具有以下权重:
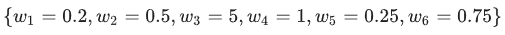
L2 正则化项为 26.915:

2- Lambda
模型开发者通过“”用正则化项的值乘以名为 lambda(又称为正则化率)的标量”的方式来调整正则化项的整体影响。
也就是说,模型开发者会执行以下运算:
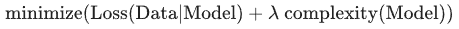
执行 L2 正则化对模型具有以下影响
- 使权重值接近于 0(但并非正好为 0)
- 使权重的平均值接近于 0,且呈正态(钟形曲线或高斯曲线)分布。
增加 lambda 值将增强正则化效果。
在选择 lambda 值时,目标是在简单化和训练数据拟合之间达到适当的平衡:
- 如果 lambda 值过高,则模型会非常简单,但是将面临数据欠拟合的风险。模型将无法从训练数据中获得足够的信息来做出有用的预测。
- 如果 lambda 值过低,则模型会比较复杂,并且将面临数据过拟合的风险。模型将因获得过多训练数据特点方面的信息而无法泛化到新数据。
注意:将 lambda 设为 0 可彻底取消正则化。在这种情况下,训练的唯一目的将是最小化损失,而这样做会使过拟合的风险达到最高。
理想的 lambda 值生成的模型可以很好地泛化到以前未见过的新数据。
遗憾的是,理想的 lambda 值取决于数据,因此需要手动或自动进行一些调整。
L2 正则化和学习速率
学习速率和 lambda 之间存在密切关联。
强 L2 正则化值往往会使特征权重更接近于 0。
较低的学习速率(使用早停法)通常会产生相同的效果,因为与 0 的距离并不是很远。
因此,同时调整学习速率和 lambda 可能会产生令人混淆的效果。
早停法指的是在模块完全收敛之前就结束训练。
在实际操作中,经常在以在线(连续)方式进行训练时采取一些隐式早停法。也就是说,一些新趋势的数据尚不足以收敛。
如上所述,更改正则化参数产生的效果可能会与更改学习速率或迭代次数产生的效果相混淆。
一种有用的做法(在训练一批固定的数据时)是执行足够多次迭代,这样早停法便不会起作用。
3- 理解
问题
1- 假设某个线性模型具有 100 个输入特征:
其中 10 个特征信息丰富。
另外 90 个特征信息比较缺乏。
假设所有特征的值均介于 -1 和 1 之间。 以下哪些陈述属实?
- L2 正则化会使很多信息缺乏的权重接近于(但并非正好是)0.0。
- L2 正则化可能会导致对于某些信息缺乏的特征,模型会学到适中的权重。
- L2 正则化会使大多数信息缺乏的权重正好为 0.0。
- L2 正则化和相关特征
2- 假设某个线性模型具有两个密切相关的特征;也就是说,这两个特征几乎是彼此的副本,但其中一个特征包含少量的随机噪点。
如果我们使用 L2 正则化训练该模型,这两个特征的权重将出现什么情况?
- 其中一个特征的权重较大,另一个特征的权重正好为 0.0。
- 这两个特征将拥有几乎相同的适中权重。
- 其中一个特征的权重较大,另一个特征的权重几乎为 0.0。
解答
1-
- 正确。L2 正则化会使权重接近于 0.0,但并非正好为 0.0。
- 正确。出乎意料的是,当某个信息缺乏的特征正好与标签相关时,便可能会出现这种情况。在这种情况下,模型会将本应给予信息丰富的特征的部分“积分”错误地给予此类信息缺乏的特征。
- L2 正则化不会倾向于使权重正好为 0.0。L2 正则化降低较大权重的程度高于降低较小权重的程度。随着权重越来越接近于 0.0,L2 将权重“推”向 0.0 的力度越来越弱。
2-
- L2 正则化几乎不会使权重正好为 0.0。相比之下, L1 正则化(稍后会介绍)则会使权重正好为 0.0。
- 正确。L2 正则化会使特征的权重几乎相同,大约为模型中只有两个特征之一时权重的一半。
- L2 正则化降低较大权重的程度高于降低较小权重的程度。因此,即使某个权重降低的速度比另一个快,L2 正则化也往往会使较大权重降低的速度快于较小的权重。
4- 关键词
泛化曲线(generalization_curve)
显示的是训练集和验证集相对于训练迭代次数的损失
过拟合 (overfitting)
创建的模型与训练数据过于匹配,以致于模型无法根据新数据做出正确的预测。
正则化 (regularization)
对模型复杂度的惩罚。正则化有助于防止出现过拟合,包含以下类型:
-
- L1 正则化
- L2 正则化
- 丢弃正则化
- 早停法(这不是正式的正则化方法,但可以有效限制过拟合)
L1 正则化 (L₁ regularization)
一种正则化,根据权重的绝对值的总和来惩罚权重。
在依赖稀疏特征的模型中,L1 正则化有助于使不相关或几乎不相关的特征的权重正好为 0,从而将这些特征从模型中移除。
与 L2 正则化相对。
L2 正则化 (L₂ regularization)
一种正则化,根据权重的平方和来惩罚权重。
L2 正则化有助于使离群值(具有较大正值或较小负值)权重接近于 0,但又不正好为 0。(与 L1 正则化相对。)
在线性模型中,L2 正则化始终可以改进泛化。
结构风险最小化 (SRM, structural risk minimization)
一种算法,用于平衡以下两个目标:
-
- 期望构建最具预测性的模型(例如损失最低)。
- 期望使模型尽可能简单(例如强大的正则化)。
例如,旨在将基于训练集的损失和正则化降至最低的函数就是一种结构风险最小化算法。
如需更多信息,请参阅 http://www.svms.org/srm/。
与经验风险最小化相对。
早停法 (early stopping)
一种正则化方法,是指在训练损失仍可以继续降低之前结束模型训练。
使用早停法时,您会在验证数据集的损失开始增大(也就是泛化效果变差)时结束模型训练。
lambda
与正则化率的含义相同。(多含义术语,在此关注的是该术语在正则化中的定义。)
正则化率 (regularization rate)
一种标量值,以 lambda 表示,用于指定正则化函数的相对重要性。从下面简化的损失公式中可以看出正则化率的影响:
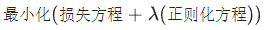
提高正则化率可以减少过拟合,但可能会使模型的准确率降低。