原文链接:https://developers.google.com/machine-learning/crash-course/introduction-to-neural-networks/
神经网络是更复杂版本的特征组合。实质上,神经网络会学习适合相应特征组合。
1- 剖析
“非线性问题”意味着无法使用形式为“$b + w_1x_1 + w_2x_2$”的线性模型准确预测标签。
对非线性问题可以用特征组合的方法进行建模。
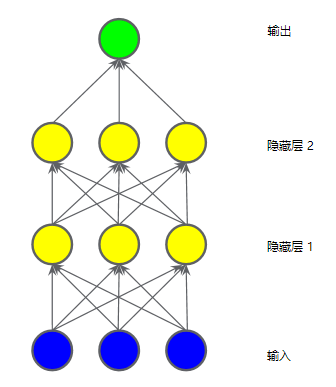
隐藏层
“隐藏层”表示中间值。
如果构建一个多层模型,“隐藏层”每个节点是上一层输入节点值的加权和,输出是“隐藏层”节点的加权和,那么此模型仍是线性的。
因为当将输出表示为输入的函数并进行简化时,只是获得输入的另一个加权和而已。
激活函数
要对非线性问题进行建模,可以直接引入非线性函数。
可以用非线性函数将每个隐藏层节点像管道一样连接起来。
在隐藏层中的各个节点的值传递到下一层进行加权求和之前,采用一个非线性函数对其进行了转换,这种非线性函数称为激活函数。
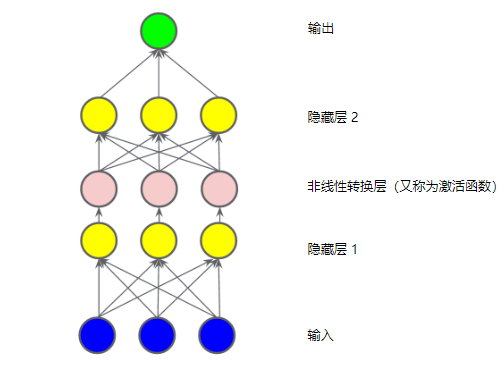
通过在非线性上堆叠非线性,能够对输入和预测输出之间极其复杂的关系进行建模。
简而言之,每一层均可通过原始输入有效学习更复杂、更高级别的函数。
常见激活函数
S型激活函数
S型激活函数将加权和转换为介于 0 和 1 之间的值。
S 型函数的响应性在两端相对较快地减少。
公式:
$F(x)=frac{1} {1+e^{-x}}$
曲线图:
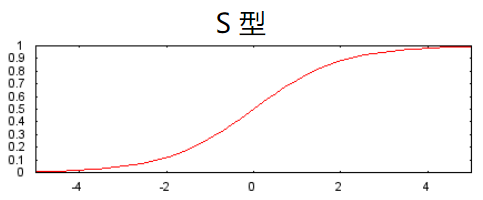
修正线性单元激活函数(简称为 ReLU)
ReLU 的优势:基于实证发现(可能由 ReLU 驱动),拥有更实用的响应范围。
相较于 S 型函数等平滑函数,效果通常要好一点,同时还非常易于计算。
公式:
$F(x)=max(0,x)$
曲线图:

其他激活函数
实际上,所有数学函数均可作为激活函数。
TensorFlow 为各种激活函数提供开箱即用型支持。建议从 ReLU 着手。
2- 总结
通常所说的“神经网络”的所有标准组件:
- 一组节点,类似于神经元,位于层中。
- 一组权重,表示每个神经网络层与其下方的层之间的关系。下方的层可能是另一个神经网络层,也可能是其他类型的层。
- 一组偏差,每个节点一个偏差。
- 一个激活函数,对层中每个节点的输出进行转换。不同的层可能拥有不同的激活函数。
3- 练习
xxx
4- 关键词
激活函数 (activation function)
一种函数(例如 ReLU 或 S 型函数),用于对上一层的所有输入求加权和,然后生成一个输出值(通常为非线性值),并将其传递给下一层。
隐藏层 (hidden layer)
神经网络中的合成层,介于输入层(即特征)和输出层(即预测)之间。神经网络包含一个或多个隐藏层。
神经网络 (neural network)
一种模型,灵感来源于脑部结构,由多个层构成(至少有一个是隐藏层),每个层都包含简单相连的单元或神经元(具有非线性关系)。
神经元 (neuron)
神经网络中的节点,通常会接收多个输入值并生成一个输出值。
神经元通过将激活函数(非线性转换)应用于输入值的加权和来计算输出值。
修正线性单元 (ReLU, Rectified Linear Unit)
一种激活函数,其规则如下:
-
- 如果输入为负数或 0,则输出 0。
- 如果输入为正数,则输出等于输入。
S 型函数 (sigmoid function)
一种函数,可将逻辑回归输出或多项回归输出(对数几率)映射到概率,以返回介于 0 到 1 之间的值。
S 型函数的公式:$y = frac{1}{1 + e^{-sigma}}$
在逻辑回归问题中, $sigma$非常简单:$sigma = b + w_1x_1 + w_2x_2 + … w_nx_n$
换句话说,S 型函数可将$sigma$转换为介于 0 到 1 之间的概率。
在某些神经网络中,S 型函数可作为激活函数使用。