卷积神经网络是如何工作的(译文)
原文:http://brohrer.github.io/how_convolutional_neural_networks_work.html
十有八九,当你听到有关深度学习又有新的技术突破的时候,总能看到卷积神经网络的影子。卷积神经网络(CNNs或ConvNets)是深度神经网络领域中的重头戏,它们在某些图像识别领域的精度甚至超过了人类。CNNs是令人激动的方法之一。
另一个让人兴奋的一点是,CNNs很容易理解,至少当你将他们分解成一些基本部分以后,它们更加容易理解。下面详细介绍。
X's and O's
一个简单的栗子:判断一张图片是X还是O。如下图:

一个理想的解决方案是保存一个X和O的图片,然后与新图片进行比较,哪个相似度高就分类为哪个。然而计算机比较实在,计算机看到的图片只是一个二维像素矩阵(设想一下大的棋盘),每个二维位置上有个数字,假设,白色为1,黑色为-1如下图。当比较的时候,一些像素不同,就会造成整个匹配不同。我们想要的效果是:不论X或O的图像如何变化,如平移、缩放、旋转或畸变等,都可以正确识别。CNNs就可以解决这个问题。

Features(特征)
CNNs比较两幅图像的方法是逐部分进行的,这些部分被称为特征。相比于全图逐像素的匹配比较,CNNs通过寻找两张图片中大致相同位置上的的粗糙特征匹配,可以更好的反映其相似度。如图所示,局部的特征相似部位。

每一个特征都可以看成一个小图片,特征匹配,就是这些特征小图的匹配。一个X字符图片,里面的对角线特征和交叉特征是几乎所有X字符都具有的,每个X的中心是一个交叉特征,而四个手臂都是对角线特征(方向不同而已)。如下图。

Convolution(卷积)
当给定一张图片,CNNs并不知道提取哪个区域的特征,于是尝试寻找图片中的所有可能的位置。在计算这些特征的时候,我们用的是一个滤波器(filter,卷积模板)。这种数学计算方法,我们用的是卷积,这是卷积神经网络名字的来历。
卷积的计算原理会使很多人觉得头疼。为了计算图像某个区域与已知特征之间的匹配关系,可以将已知特征矩阵(卷积模板)内的每个像素值与对应图像中的像素值进行乘法运算,然后将每个像素的计算结果相加,再除以特征矩阵(卷积模板)中总的像素个数。假设像素都是白的(上面图中的案例),也就是1,那么乘积还是1,都是-1,乘积也是1,只有当不匹配的时候,才是-1。如果特征与图像中对应位置的特征都一样,那么最终的计算结果会得到1(本案例结果)。反之小于1。

继续这个计算过程,让特征矩阵(卷积模板)与所有可能的图像区域进行卷积运算。最终通过每一次卷积操作得到的值会构成一个新的二维矩阵,这个矩阵是图像中找到的特征的映射图,值越接近1,说明特征越匹配,越接近-1,说明更接近负的特征(相片的底片原理),接近0,说明不存在任何匹配关系。
接着,将其他特征矩阵(实例图中的其他对角线特征、交叉特征等)与图像进行相同的操作,最终得到几个特征图,每个特征图对应一个卷积模板。这些操作都可以在CNNs的卷积层完成。

很容易理解CNNs是进行了无所顾忌的(贪婪的进行全部像素的卷积运算)运算来保持其识别能力的,尽管我们可以很简单的将CNN写在纸上,很快的将其加法、乘法、除法的数量写出来。用数学语言来描述,就是卷积网络的计算复杂度与图像的像素数目、卷积模板的像素数目以及卷积模板的个数具有线性比例关系。现在的计算芯片(CPU、GPU等)可以轻松的解决大规模卷积计算问题,这也是CNNs最近才火起来的原因。
Pooling(下采样)
除了卷积层,另一个有力工具是pooling层,pooling是一种在保留图像大部分重要信息的基础上缩小图像的方法。其背后的数学原理很简单(小学二年级水平?),包括一个滑动窗口(n*n)遍历整幅图像,然后取这窗口中所有像素的最大(max pooling)或平均(average pooling)或随机(random pooling)等等值。下图是max pooling。一般在实际操作中,2x2、3x3的pooling 窗口并且以2个像素为步长的pooling 操作效果最佳。

按照2x2的pooling窗口,最终得到的图像是原图的四分之一。由于pooling取的是窗口的最大值,所以它保留了窗口中的最佳特征。这意味着其不关心在pooling窗口中特征吻合在哪个很精确的像素级位置,只要待测特征与窗口中某个位置的特征吻合即可。这样的结果使得CNNs可以发现图像中是否存在某一特征而不用关心它具体在哪。这就解决了计算机比较实在的问题(让计算机不要精确的知道特征在哪,如果精确的知道特征在哪个位置,那泛化能力很弱)。
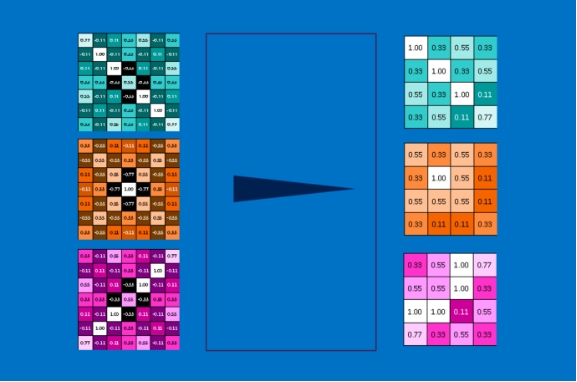
Pooling操作是在图像或者图像集合上进行的,所以输出后的结果图像数目没有变化,只是像素数目减少了。这样就减少了数据量,比如一个8M的图像,pooling操作后就成了2M大小,易于后面的计算操作。
Rectified Linear Units (ReLU)
ReLU操作(即一种激活函数),这个CNNs组成成员很小但很重要。其背后的数学原理也很简单:当一个输入值为负数,经过ReLU函数后输出为0。
这个操作使得CNN可以保持数学上的健壮性,学习的值范围从0到无穷大(只在单侧抑制,具有稀疏性,兴奋边界很宽等)。这就像是CNNs大车的车轴润滑剂,简单而不华丽,但缺少它大车将无法走的更远。
ReLU层的输出和输入同尺寸大小,只是所有的负数变成了0。

Deep learning(深度学习)
通过前面,可以发现,每一层的输入与输出非常相似(都是二维矩阵),正是因为如此,我们可以像搭建乐高积木一样将它们堆叠起来。一幅原始图像,经过卷积滤波、ReLU矫正和pooling操作,可以得到一系列的缩小后的特征图像。这个过程可以一直重复下去,这样就会得到更多和更复杂的特征图,并且图像变得更小,数据得到更大的压缩。
这样的结构,使得低特征提取层可以提取图像的简单特征,比如边缘,亮度信息等局部特征,如下左图。更高的特征提取层将逐步提取图像的高级特征,比如形状和图案,这样逐渐容易分辨。比如,在CNN人脸识别中,最高层的特征就和人脸很相近了,如下右图。
Fully connected layers(全连接层)
CNNs的一个利器是全连接层,它将图像的高级特征图转化为投票数,在我们的栗子中,就是投票识别X和O。全连接层是传统神经网络的主要组成层,输入的不是二维矩阵,而是每个元素同等重要的一个单列,每个值拥有自己的投票权利,是X还是O。但这不公平,因为有些值相比其它值更能反映这个图像是X,有些更能反映它是O,而这些有突出表现的值就应该有更高的投票权利。这些所谓的投票权利,就是特征值和类别之间的权值,或者说是连接能力。当一个原始图像进入CNN后,从低层一直到全连接层,一个所谓的投票就开始了,最终的输出类别就是得票数最高的那个类别。

犀利的全连接层自然也可以堆叠了(输出和输入相似,都是一个值列表)。实际情况下,经常几个全连接层连接在一起,中间的算是投票给隐含层的类别。这样,每个额外的层让网络学到了丰富且复杂的联合特征,这样使得网络的预测精度更高。
Backpropagation(后向传播)
到这里,故事很完美,但却有些疑问:特征从哪来?我们如何在全连接层中找到的这些权值?手动的?肯定不是,否则CNNs将不会这么火。其实是后向传播方法帮助我们实现了这些操作。
为了应用后向传播方法,我们必须准备大量的已知标签的图像,就像是大量的已知是X字符图片和是O的图片,而准备数据则需要很大的耐心。我们用这些数据和一个未训练的神经网络(未训练的意思是,每个特征模板的像素值和全连接层的权值都是随机数)。然后将这些图像去输入未训练的神经网络。
每个图像经过CNN处理后都得到一个类别投票,而投票类别错误(本该是X,投成O)的总数,也就是误差,是评判我们的特征模板和权值好坏的依据。接下来,通过调整特征模板和权值,降低这个误差。调节的值(变化的值)都是正负成对的,也就是权值加一点和权值减一点两个情况都要尝试,然后再各自计算误差值。如果发现这两者中哪个误差减少了,那就保留(增或减的)哪个值。如此过程应用在卷积层中的特征模板像素值和全连接层上的权值上,新的权值最终使得误差略有降低。然后再应用在不同的已知标签图像上,再经过很多很多次迭代后,在一张图像上的权值可能会被覆盖丢失,但是符合整个大数据集的权值和特征将会留存(个体虽有差异、但整体大势所趋)。只要数据足够多,就可以得到泛化能力强的网络模型。

当然,显而易见的是,后向传播运算量大,需要更高的硬件计算能力。(这也是深度学习中常用离线训练,在线识别的原因)
Hyperparameters(超参数)
CNNs仍然有很多值得考虑的问题:
(1)每个卷积层,需要多少特征数?每个特征图有多少像素?
(2)每个pooling层,窗口大小是多少?步长呢?
(3)每个全连接层,应该有多少隐含层神经元?
还有更高级的架构问题需要解决:网络中每一层的个数?如何组织?有些深度神经网络有上千层,可以预测更多类别可能性。
CNN结构的排列组合太多太多,只有部分被测试过。CNN的发展壮大离不开社区的推动,经常得到一些令人惊喜的结果。我们尝试了一些简单的CNN,还有很多很多的CNN结构,比如拥有一些新的类型层,更复杂的层之间的互联方式等等。
Beyond images(除图像之外)
CNN不止可以分类图像文件,还可以分类其它数据类型。只要将这种数据类型转换为类似图像就可以了(矩阵形式?)。例如,声音信号,可以被切割成短的时间块,然后将每块分解成低音、中音、高音或更细的频带。这样就可以将其看做是个二维矩阵,每一列为一个时间块,每一行为一个频带。如下图。
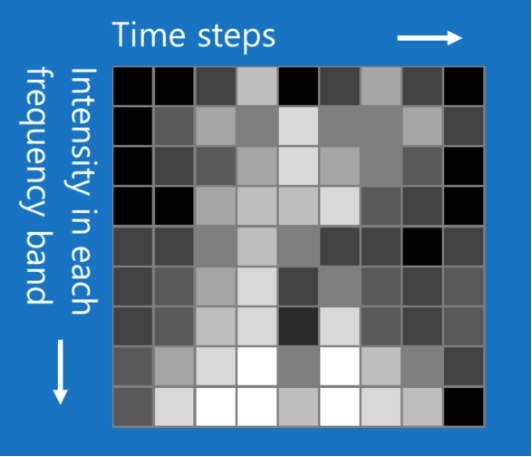
这样看起来就像图像了。CNNs对这种数据也能有很好的表现。还有像自然语言处理中的文本数据,甚至是医药发现中的化学数据等等。
没有万能的技术,所以也有不适合CNNs的数据类型,比如客户数据。每一行表示一个客户,每一列表示客户相关信息,比如姓名,性别,地址,邮箱,购物和浏览历史等。这样的数据,行和列的位置关系不再重要。这样的话,行可以重新排列,列也可以重新排序,而不会损失重要数据。相反地,重新排列图像的行列将使得图像几乎变得杂乱无章,没有用处。
经验法则:如果你的数据交换行列后一样有用,那么就不适合用CNNs。反之,如果你的问题就像是在一张图像中寻找一些图案,那么CNNs就是你想要的。
Learn more(学无止境)
继续挖掘Deep Learning,有很多资料可以借鉴:
http://brohrer.github.io/deep_learning_demystified.html
http://cs231n.github.io/convolutional-networks/
http://colah.github.io/archive.html
还有很多优秀的框架值得动手操作:
· Caffe
· CNTK
· Theano
· Torch


