Leetcode Binary Tree Inorder Traversal

Given a binary tree, return the inorder traversal of its nodes' values.

For example:
Given binary tree {1,#,2,3},

   1
    
     2
    /
   3 

return [1,3,2].

Note: Recursive solution is trivial, could you do it iteratively?

---

解题思路：

In-order (symmetric)

1. Traverse the left subtree by recursively calling the in-order function
2. Display the data part of root element (or current element)
3. Traverse the right subtree by recursively calling the in-order function

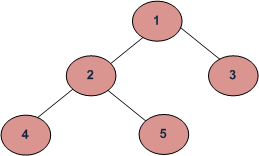 Inorder traversal for the given figure is 4 2 5 1 3.

两种方法：1）recursive 2) iterative, 用stack

---

Java code:

1. recursive

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<Integer>();
        if(root != null){
            result.addAll(inorderTraversal(root.left));
            result.add(root.val);
            result.addAll(inorderTraversal(root.right));
        }
        return result;
    }
}

2. iterative

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new LinkedList<Integer>();
        Stack<TreeNode> s = new Stack<TreeNode>();
        while(!s.isEmpty() || root != null){
           if(root != null){
               s.push(root);
               root = root.left;
           }else{
               root = s.pop();
               result.add(root.val);
               root = root.right;
           }
        }
        return result;
    }
}

---

20160602

recursion

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //inorder: left subtree - root - right subtree
        List<Integer> result = new ArrayList<Integer>();
         inorderTraversal(root, result);
         return result;
    }
    
    private void inorderTraversal(TreeNode root, List<Integer> list) {
        if(root == null) {
            return;
        }
        inorderTraversal(root.left, list);
        list.add(root.val);
        inorderTraversal(root.right, list);
    }
}

Reference:

1. http://www.geeksforgeeks.org/618/

2. https://leetcode.com/discuss/64937/inorder-traversal-java-solution-both-iteration-recursion