初涉差分约束系统

一个把数学问题转化为图论模型的很好的例子

差分约束系统

差分约束系统的定义是：一个由$n$个变量和$m$个约束条件组成，形成$m$个形如$x_i-x_j≤k$的不等式($i,j∈[1,n],k$为常数)的系统。

举个例子（图自网络）：

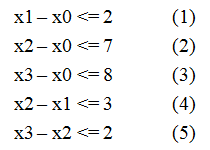
例如这个不等式组就是一个差分约束系统。

我们要求的通常是附加几个条件之后（例如$x_i>0$）的这个系统的最大/小解。因为很容易发现，若只有变量之间的相对限制，这个系统要么是无数解；要么是无解。

那么怎么把这个抽象的不等式组化为图论模型呢？

观察一下这个例子（图仍然来自网络）：

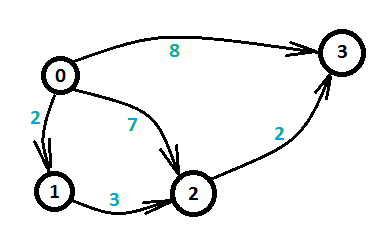
这个例子其实就是上面那个不等式组的图论描述。其中图中的边$(u,v,w)$表示$x_v-x_u≤w$。

那么当要求最大值时，就求一遍最短路就好了。

看上去是不是很奇怪，为什么求最大值时要求最短路呢？

因为这里的所有约束条件是必须要同时满足的，所以求的最短路就是满足所有条件下的最大值了。

于是就变为了一张图中的最长/短路问题了。

值得注意的是由于差分约束中会有负权，所以应该使用SPFA来解决。

参考：

1.夜深人静写算法（四） - 差分约束

2.BZOJ 2330: [SCOI2011]糖果 [差分约束系统] 【学习笔记】

一些题目

【线性约束】排队

题目描述

有N个人按顺序排成一条直线，满足任何两个人的位置不重合，现在有两种约束：
X约束Ax Bx Cx(1 <= Ax < Bx <= N)，表示Ax和Bx的距离小于等于Cx。
Y约束Ay By Cy(1 <= Ay < By <= N)，表示Ay和By的距离大于等于Cy。
如果这样的排列存在，输出总和最长距离（无限则输出INF）。
否则如果不存在，输出-1。

---

题目分析

建图的要点上文已经提到过了，这里讲一下怎么判断无限长。

这里求的是最大值，也就是说我们跑的是最短路。没有最大值等价于没有最短路。

显然没有最短路就是存在负权环，刚好SPFA顺带解决了这个问题。

【区间约束】luoguP1645 序列

题目描述

有一个整数序列，它的每个数各不相同，我们不知道它的长度是多少（即整数个数），但我们知道在某些区间中间至少有多少个整数，用区间（Li,Ri,Ci）来描述，表示这个整数序列中至少有Ci个数来自区间[Li,Ri]，给出若干个这样的区间，问这个整数序列的长度最少能为多少？

输入输出格式

输入格式：

第一行一个整数N，表示区间个数；

接下来N行，每行三个整数（Li,Ri,Ci），描述一个区间。

输出格式：

仅一个数，表示该整数序列的最小长度。

【数据规模】

N<=1000，0<=Li<=Ri<=1000,1<=Ci<=Ri-Li+1

---

题目大意

这里讲一下大致题意（好像是出题人语文不大好写的不是人话？也可能是我语文不好看不懂？）

现在有一个长为1000单位长度的区间，单位长度内要么有一个数，要么什么都没有。

现在知道一些小区间内至少有多少数，求大区间内最少有多少数。

题目分析

区间问题套路：前缀和。

我们对于前缀和进行差分约束。

这里求的是最小值=最长路。

#include<bits/stdc++.h>
const int maxn = 1013;

struct node
{
    int y,val;
    node() {}
    node(int a, int b):y(a),val(b) {} 
};
int n,m;
int dis[maxn];
bool vis[maxn];
std::vector<node> a[maxn];
std::queue<int> q;

int read()
{
    char ch = getchar();
    int num = 0;
    for (; !isdigit(ch); ch = getchar());
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    return num;
}
void spfa(int s)
{
    q.push(s);
    memset(dis, -63, sizeof dis);
    dis[s] = 0;
    while (q.size())
    {
        int tt = q.front();
        vis[tt] = 0;
        q.pop();
        for (unsigned int i=0; i<a[tt].size(); i++)
            if (dis[a[tt][i].y] < dis[tt]+a[tt][i].val)　//最长路
            {
                dis[a[tt][i].y] = dis[tt]+a[tt][i].val;
                if (!vis[a[tt][i].y]){
                    vis[a[tt][i].y] = 1;
                    q.push(a[tt][i].y);
                } 
            }
    }
}
int main()
{
    m = read();
    for (int i=1; i<=m; i++)
    {
        int x = read()+1, y = read()+1
        , z = read();
        n = std::max(n, y);
        a[x-1].push_back(node(y, z));
    }
    for (int i=1; i<=n; i++)
        a[i-1].push_back(node(i, 0)),　　　　　　//相邻前缀和之间也有限制
        a[i].push_back(node(i-1, -1));  //这是为了避免f[i]=f[i-1]+k(k>1)的情况
    spfa(0);
    printf("%d
",dis[n]);
    return 0;
}

【区间约束】bzoj2330: [SCOI2011]糖果

Description

幼儿园里有N个小朋友，lxhgww老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候，lxhgww需要满足小朋友们的K个要求。幼儿园的糖果总是有限的，lxhgww想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。

Input

输入的第一行是两个整数N，K。

接下来K行，表示这些点需要满足的关系，每行3个数字，X，A，B。

如果X=1， 表示第A个小朋友分到的糖果必须和第B个小朋友分到的糖果一样多；

如果X=2， 表示第A个小朋友分到的糖果必须少于第B个小朋友分到的糖果；

如果X=3， 表示第A个小朋友分到的糖果必须不少于第B个小朋友分到的糖果；

如果X=4， 表示第A个小朋友分到的糖果必须多于第B个小朋友分到的糖果；

如果X=5， 表示第A个小朋友分到的糖果必须不多于第B个小朋友分到的糖果；

Output

输出一行，表示lxhgww老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出-1。

【数据范围】

    对于30%的数据，保证 N<=100

    对于100%的数据，保证 N<=100000

对于所有的数据，保证 K<=100000，1<=X<=5，1<=A, B<=N

---

题目分析

看上去稍微复杂了一点？

这里出现了严格的不等式，不过由于这里的所有值都是整数，我们可以将$a<b$变为$a≤b-1$。

再者在建图的地方注意一下、判断一下无解，就可以了。

这里有一篇写得非常好的博客：BZOJ 2330: [SCOI2011]糖果 [差分约束系统] 【学习笔记】，里面有一些非常妙的注意点。

#include<bits/stdc++.h>
const int maxn = 100033;

struct node
{
    int y,val;
    node() {}
    node(int a, int b):y(a),val(b) {}
};
int n,k;
int dis[maxn],tot[maxn];
long long cnt;
bool vis[maxn];
std::queue<int>    q;
std::vector<node> a[maxn];

int read()
{
    char ch = getchar();
    int num = 0;
    for (; !isdigit(ch); ch = getchar());
    for (; isdigit(ch); ch = getchar())
        num = (num<<1)+(num<<3)+ch-48;
    return num;
}
void end()
{
    puts("-1");
    exit(0);
}
bool spfa()
{
    for (int i=1; i<=n; i++)
    {
        vis[i] = 1, dis[i] = 1, tot[i] = 1;
        q.push(i);
    }
    while (q.size())
    {
        int tt = q.front();
        vis[tt] = 0;
        q.pop();
        for (unsigned int i=0; i<a[tt].size(); i++)
        {
            int v = a[tt][i].y, w = a[tt][i].val;
            if (dis[v] < dis[tt]+w)
            {
                dis[v] = dis[tt]+w;
                if (!vis[v]){
                    vis[v] = 1;
                    if (++tot[v] > n) return 1;
                    q.push(v);
                }
            }
        }
    }
    return 0;
}
int main()
{
    n = read(), k = read();
    for (int i=1; i<=k; i++)
    {
        int tt = read(), x = read(), y = read();
        if (tt==1 || tt==3)
            a[y].push_back(node(x, 0));
        if (tt==1 || tt==5)
            a[x].push_back(node(y, 0));
        if (tt==2)
        {
            if (x==y) end();
            else a[x].push_back(node(y, 1));
        }
        if (tt==4)
        {
            if (x==y) end();
            else a[y].push_back(node(x, 1));
        }
    }
    if (spfa()) end();
    for (int i=1; i<=n; i++) cnt += dis[i];
    printf("%lld
",cnt);
    return 0;
}

【未知条件约束】poj1275Cashier Employment

题目链接：http://poj.org/problem?id=1275

现在还不会……

END