久仰字符串系列理论
KMP
讲解(引用自bzoj3670动物园)
某天,园长给动物们讲解KMP算法。
园长:“对于一个字符串S,它的长度为L。我们可以在O(L)的时间内,求出一个名为next的数组。有谁预习了next数组的含义吗?”
熊猫:“对于字符串S的前i个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作next[i]。”
园长:“非常好!那你能举个例子吗?”
熊猫:“例S为abcababc,则next[5]=2。因为S的前5个字符为abcab,ab既是它的后缀又是它的前缀,并且找不到一个更长的字符串满足这个性质。同理,还可得出next[1] = next[2] = next[3] = 0,next[4] = next[6] = 1,next[7] = 2,next[8] = 3。”
作用
基础KMP算法是用来处理字符串匹配的问题的。最简单的应用便是纯粹的询问:A是否在B中出现过。
KMP最核心的内容莫过于fail[](也叫做next[])。对于这部分内容的理解可以考出比较多的花样(但似乎kmp的模型无非比较经典的那几个,我到现在为止见过最灵活的还是非主席树莫属)
KMP的例题
【kmp模板】P3375 【模板】KMP字符串匹配
题目描述
如题,给出两个字符串s1和s2,其中s2为s1的子串,求出s2在s1中所有出现的位置。
为了减少骗分的情况,接下来还要输出子串的前缀数组next。
(如果你不知道这是什么意思也不要问,去百度搜[kmp算法]学习一下就知道了。)
输入输出格式
输入格式:
第一行为一个字符串,即为s1
第二行为一个字符串,即为s2
输出格式:
若干行,每行包含一个整数,表示s2在s1中出现的位置
接下来1行,包括length(s2)个整数,表示前缀数组next[i]的值。
说明
时空限制:1000ms,128M
数据规模:
设s1长度为N,s2长度为M
对于30%的数据:N<=15,M<=5
对于70%的数据:N<=10000,M<=100
对于100%的数据:N<=1000000,M<=1000000
样例说明:
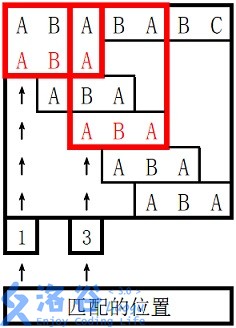
所以两个匹配位置为1和3,输出1、3
题目分析
基础KMP板子,先存着。
1 #include<bits/stdc++.h> 2 const int maxn = 1000035; 3 4 char A[maxn],B[maxn]; 5 int fail[maxn],n,m; 6 7 int main() 8 { 9 scanf("%s%s",A+1,B+1); 10 n = strlen(A+1), m = strlen(B+1); 11 fail[1] = 0; 12 for (int i=1, j=0; i<m; i++) 13 { 14 while (j&&B[j+1]!=B[i+1]) j = fail[j]; //不能继续匹配并且j没减到0,j回退 15 if (B[j+1]==B[i+1]) j++; //能继续匹配 16 fail[i+1] = j; 17 } 18 for (int i=0, j=0; i<n; i++) 19 { 20 while (j&&B[j+1]!=A[i+1]) j = fail[j]; //不能继续匹配并且j没减到0,j回退 21 if (B[j+1]==A[i+1]) j++; //能匹配 22 if (j==m){ //匹配到了B串 23 printf("%d ",i-m+2); 24 j = fail[j]; //继续找匹配(因为有可能两处匹配重叠) 25 } 26 } 27 for (int i=1; i<=m; i++) printf("%d ",fail[i]); 28 puts(""); 29 return 0; 30 }
【kmp略带理解】hdu2087剪花布条
Problem Description
Input
Output
题目分析
大意就是要在A中找出最多数量互不重叠的B串。于是每一次匹配完是将j清零就好了。
1 #include<bits/stdc++.h> 2 const int maxn = 1003; 3 4 char A[maxn],B[maxn]; 5 int fail[maxn],n,m,ans; 6 7 int main() 8 { 9 while (scanf("%s",A+1)!=EOF) 10 { 11 if (A[1]=='#') break; 12 scanf("%s",B+1); 13 n = strlen(A+1), m = strlen(B+1); 14 ans = fail[1] = 0; 15 for (int i=1, j=0; i<m; i++) 16 { 17 while (j&&B[i+1]!=B[j+1]) j = fail[j]; 18 if (B[i+1]==B[j+1]) j++; 19 fail[i+1] = j; 20 } 21 for (int i=0, j=0; i<n; i++) 22 { 23 while (j&&A[i+1]!=B[j+1]) j = fail[j]; 24 if (A[i+1]==B[j+1]) j++; 25 if (j==m) 26 ans++, j = 0; 27 } 28 printf("%d ",ans); 29 } 30 return 0; 31 }
【kmp理解】bzoj3670: [Noi2014]动物园
Description
近日,园长发现动物园中好吃懒做的动物越来越多了。例如企鹅,只会卖萌向游客要吃的。为了整治动物园的不良风气,让动物们凭自己的真才实学向游客要吃的,园长决定开设算法班,让动物们学习算法。
某天,园长给动物们讲解KMP算法。
园长:“对于一个字符串S,它的长度为L。我们可以在O(L)的时间内,求出一个名为next的数组。有谁预习了next数组的含义吗?”
熊猫:“对于字符串S的前i个字符构成的子串,既是它的后缀又是它的前缀的字符串中(它本身除外),最长的长度记作next[i]。”
园长:“非常好!那你能举个例子吗?”
熊猫:“例S为abcababc,则next[5]=2。因为S的前5个字符为abcab,ab既是它的后缀又是它的前缀,并且找不到一个更长的字符串满足这个性质。同理,还可得出next[1] = next[2] = next[3] = 0,next[4] = next[6] = 1,next[7] = 2,next[8] = 3。”
园长表扬了认真预习的熊猫同学。随后,他详细讲解了如何在O(L)的时间内求出next数组。
下课前,园长提出了一个问题:“KMP算法只能求出next数组。我现在希望求出一个更强大num数组一一对于字符串S的前i个字符构成的子串,既是它的后缀同时又是它的前缀,并且该后缀与该前缀不重叠,将这种字符串的数量记作num[i]。例如S为aaaaa,则num[4] = 2。这是因为S的前4个字符为aaaa,其中a和aa都满足性质‘既是后缀又是前缀’,同时保证这个后缀与这个前缀不重叠。而aaa虽然满足性质‘既是后缀又是前缀’,但遗憾的是这个后缀与这个前缀重叠了,所以不能计算在内。同理,num[1] = 0,num[2] = num[3] = 1,num[5] = 2。”
最后,园长给出了奖励条件,第一个做对的同学奖励巧克力一盒。听了这句话,睡了一节课的企鹅立刻就醒过来了!但企鹅并不会做这道题,于是向参观动物园的你寻求帮助。你能否帮助企鹅写一个程序求出num数组呢?
特别地,为了避免大量的输出,你不需要输出num[i]分别是多少,你只需要输出![]() 对1,000,000,007取模的结果即可。
对1,000,000,007取模的结果即可。
![]()
Input
第1行仅包含一个正整数n ,表示测试数据的组数。随后n行,每行描述一组测试数据。每组测试数据仅含有一个字符串S,S的定义详见题目描述。数据保证S 中仅含小写字母。输入文件中不会包含多余的空行,行末不会存在多余的空格。
Output
包含 n 行,每行描述一组测试数据的答案,答案的顺序应与输入数据的顺序保持一致。对于每组测试数据,仅需要输出一个整数,表示这组测试数据的答案对 1,000,000,007 取模的结果。输出文件中不应包含多余的空行。
Sample Input
aaaaa
ab
abcababc
Sample Output
1
32
HINT
n≤5,L≤1,000,000
题目大意
kmp算法中所求的$fail[i]$代表$i$位置最长「相同的前缀后缀」;相似地,这里的$num[i]$代表$i$位置所有不重叠「相同的前缀后缀」的数量和。
题目分析
嘛……算是一道考察对于kmp算法理解的思维题。
每一次求next[]时舍去有重叠的最长前后缀是不行的,因为会对后面的转移造成影响。
那么考虑最基础的暴力,就是枚举每一个i再做kmp(感觉这个暴力可以用exKMP优化的样子,不过我不会)。显然复杂度是爆炸的。
继而考虑优化,先求出允许重叠的「相同的前缀后缀」的答案$prenum[]$,再考虑与当前情况不矛盾的$prenum[]$之和。这句话或许有点奇怪,换而言之就是:在之前允许重叠的答案里,找出一些对于当前情况来说,不重叠的答案之和。
好吧之后的过程我讲得就不甚清楚了,挂一篇博客吧[NOI2014][bzoj3670] 动物园 [kmp+next数组应用]
1 #include<bits/stdc++.h> 2 const int maxn = 1000035; 3 const int MO = 1e9+7; 4 5 int prenum[maxn],fail[maxn]; 6 int tt,n,ans; 7 char str[maxn]; 8 9 int main() 10 { 11 scanf("%d",&tt); 12 while (tt--) 13 { 14 memset(fail, 0, sizeof fail); 15 scanf("%s",str); 16 n = strlen(str); 17 prenum[0] = 0, prenum[1] = 1, ans = 1; 18 for (int i=1, j=0; i<n; i++) 19 { 20 while (j&&str[i]!=str[j]) j = fail[j]; 21 if (str[i]==str[j]) j++; 22 fail[i+1] = j, prenum[i+1] = prenum[j]+1; 23 } 24 for (int i=1, j=0; i<n; i++) 25 { 26 while (j&&str[i]!=str[j]) j = fail[j]; 27 if (str[i]==str[j]) j++; 28 while ((j<<1)>i+1) j = fail[j]; 29 ans = 1ll*ans*(prenum[j]+1)%MO; 30 } 31 printf("%d ",ans); 32 } 33 return 0; 34 }
【完全最短循环子串】poj2406Power Strings
Description
Input
Output
Sample Input
abcd
aaaa
ababab
.
Sample Output
1
4
3
Hint
题目大意
多组数据,求一个字符串的最短循环子串
题目分析
注意到kmp中的$fail[i]$表示的是最大的前缀的后缀的长度,即$1...fail[n]$等同$n-fail[n]+1...n$。也就是说若原串是一个循环次数大于1的循环子串,那么$n-fail[n]$一段刚好是最短的循环子串。
当时我也想了一会儿才想清楚,这里放一张图。
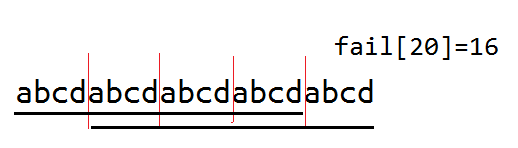
1 #include<cstring> 2 #include<cstdio> 3 const int maxn = 1000035; 4 5 char ch[maxn]; 6 int fail[maxn],n; 7 8 int main() 9 { 10 while (scanf("%s",ch+1)) 11 { 12 if (ch[1]=='.') break; 13 memset(fail, 0, sizeof fail); 14 n = strlen(ch+1); 15 for (int i=1, j=0; i<n; i++) 16 { 17 while (j&&ch[i+1]!=ch[j+1]) j = fail[j]; 18 if (ch[i+1]==ch[j+1]) j++; 19 fail[i+1] = j; 20 } 21 if (n%(n-fail[n])==0) printf("%d ",n/(n-fail[n])); 22 else puts("1"); 23 } 24 return 0; 25 }
【不完全最短循环子串】bzoj1355: [Baltic2009]Radio Transmission
Description
Input
Output
Sample Input
cabcabca
Sample Output
HINT
对于样例,我们可以利用"abc"不断自我连接得到"abcabcabc",读入的cabcabca,是它的子串
题目分析
数据保证了给定串为不完整的循环子串,那么算几组手造数据的$fail[]$会发现:
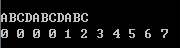
第二次循环节开始时,fail[]变为从一开始的递增序列。
要注意的是这并不意味着答案就是从首开始的零个数。
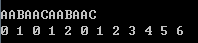
这是一个小细节。
1 #include<bits/stdc++.h> 2 const int maxn = 1000035; 3 4 char ch[maxn]; 5 int n,fail[maxn]; 6 7 int main() 8 { 9 scanf("%d%s",&n,ch+1); 10 for (int i=1, j=0; i<n; i++) 11 { 12 while (j&&ch[i+1]!=ch[j+1]) j = fail[j]; 13 if (ch[i+1]==ch[j+1]) j++; 14 fail[i+1] = j; 15 } 16 printf("%d ",n-fail[n]); 17 return 0; 18 }
【fail[]巧妙运用】bzoj1511: [POI2006]OKR-Periods of Words
Description
Input
Output
Sample Input
babababa
Sample Output
题目分析
好困,大脑宕机。
先挂题解和代码:luoguP3435 [POI2006]OKR-Periods of Words
1 #include<bits/stdc++.h> 2 const int maxn = 1000035; 3 4 int n,fail[maxn]; 5 char str[maxn]; 6 long long ans; 7 8 int main() 9 { 10 scanf("%d%s",&n,str+1); 11 for (int i=1, j=0; i<n; i++) 12 { 13 while (j&&str[i+1]!=str[j+1]) j = fail[j]; 14 if (str[i+1]==str[j+1]) j++; 15 fail[i+1] = j; 16 } 17 for (int i=1; i<=n; i++) 18 if (fail[fail[i]]) fail[i] = fail[fail[i]]; 19 for (int i=1; i<=n; i++) 20 if (fail[i]) ans += 1ll*i-fail[i]; 21 printf("%lld ",ans); 22 return 0; 23 }
END