【哈希二分】bzoj2084: [Poi2010]Antisymmetry

可以用manacher或者SA搞过去的；非常有趣的hash题

Description

对于一个01字符串，如果将这个字符串0和1取反后，再将整个串反过来和原串一样，就称作“反对称”字符串。比如00001111和010101就是反对称的，1001就不是。
现在给出一个长度为N的01字符串，求它有多少个子串是反对称的。

Input

第一行一个正整数N (N <= 500,000)。第二行一个长度为N的01字符串。

Output

一个正整数，表示反对称子串的个数。

Sample Input

8
11001011

Sample Output

hint

7个反对称子串分别是：01(出现两次), 10(出现两次), 0101, 1100和001011

题目分析

暂时只会哈希做法……

观察到一个性质：若一个区间为反对称子串，那么这个子串的任意一个子串也是反对称子串。并且奇数长度的区间是一定非法的。

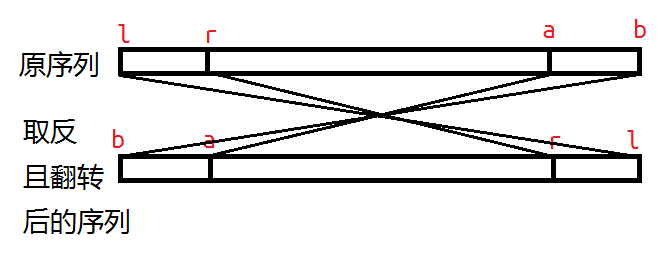
有了这个单调性，就能够枚举中间点，对最长子串长度进行二分了。

 1 #include<bits/stdc++.h>
 2 typedef unsigned long long ull;
 3 const int maxn = 500035;
 4 const ull base = 233;
 5 
 6 int n;
 7 char s[maxn];
 8 ull power[maxn],lhsh[maxn],rhsh[maxn],ans;
 9 
10 bool equal(int l, int r)
11 {
12     return lhsh[r]-lhsh[l]*power[r-l]==rhsh[l]-rhsh[r]*power[r-l];
13 }
14 int main()
15 {
16     scanf("%d%s",&n,s+1);
17     power[0] = 1;
18     for (int i=1; i<=n; i++)
19         power[i] = power[i-1]*base, lhsh[i] = (lhsh[i-1]*base)+(s[i]-'0');
20     for (int i=n; i; i--)
21         rhsh[i] = (rhsh[i+1]*base)+1-(s[i]-'0');
22     for (int i=1; i<=n; i++)
23     {
24         int l = 1, r = std::min(i, n-i), pos = 0;
25         for (int mid=(l+r)>>1; l<=r; mid=(l+r)>>1)
26             if (equal(i-mid+1, mid+i)) l = mid+1, pos = mid;
27             else r = mid-1;
28         ans += pos;
29     }
30     printf("%lld
",ans);
31     return 0;
32 }

此外还有改进的manacher做法？

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int maxx=500002;
 4 int n,f[maxx],mid=1,r=1;
 5 long long ans;
 6 char s[maxx];
 7 int main(){
 8 //    freopen("x.in","r",stdin);
 9     scanf("%d%s",&n,s+1);s[0]=s[n+1]='9';
10     for(int i=2;i<=n;i++){
11         if(i<r)f[i]=min(r-i+1,f[(mid<<1)-i]);else f[i]=0;
12         while(abs(s[i+f[i]]-s[i-f[i]-1])==1)++f[i];
13         if(i+f[i]-1>r)mid=i,r=i+f[i]-1;
14         ans+=f[i];
15     }
16     printf("%lld",ans);
17     return 0;
18 }

copyright @MikuKnight

END

【哈希 二分】bzoj2084: [Poi2010]Antisymmetry