全网好像就只有劼和manchery写了博客的样子……;正解可能是最大流?但是仔细特判也能过
题目描述
RMQ问题即区间最值问题是一个有趣的问题。
在这个问题中,对于一个长度为 n 的排列,query(l,r) 将返回 al,⋯,ar 中的最大值。
如对于 {3,1,4,2,5},query(2,4)=max(1,4,2)=4
现在我们给出 m 次询问的结果,问是否存在至少一个长度为 n 的排列 P 满足所有的条件。
输入格式
第一行 T
每一组数据中,第一行 n,m,接下来 m 行,每行 li,ri,ans
输出格式
T 行 Possible 或 Impossible
数据范围
对于 20% 的数据, n≤10
对于另 10% 的数据,li=ri
对于另 20% 的数据,[li,ri] 两两没有交集
对于另 20% 的数据,ansi 互不相同
对于所有数据,T≤10,n,m≤2000,1≤li≤ri≤n
时间限制 1s
空间限制 256MB
官方题解
先按照值从小到大排序
然后值一样的一起处理 如果交为空 无解
如果交被之前所有的并给完全包含了 无解
如果某一时刻并的大小比数字还大 无解
以上三点就是充要条件
题目分析
manchery的题解是比较详细的,但似乎漏了点什么
比如说这种情况:
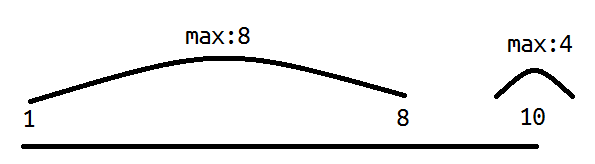
就是不可以的。
第一遍做这题的时候有考虑到两个问题:
- 区间最大值不够这个区间用(manchery第三条条件)
- 空余位置不足够填下剩下的数字(以上的反例)
不过由于代码能力不足,并没有打出来……
1 #include<bits/stdc++.h> 2 const int maxn = 2003; 3 4 struct point 5 { 6 int l,r,c; 7 }a[maxn],b[maxn],t[maxn]; 8 int T,n,m,stb; 9 bool pot[maxn],fbd[maxn][maxn],insideConflict; 10 11 int read() 12 { 13 char ch = getchar(); 14 int num = 0; 15 bool fl = 0; 16 for (; !isdigit(ch); ch = getchar()) 17 if (ch=='-') fl = 1; 18 for (; isdigit(ch); ch = getchar()) 19 num = (num<<1)+(num<<3)+ch-48; 20 if (fl) num = -num; 21 return num; 22 } 23 int main() 24 { 27 T = read(); 28 while (T--) 29 { 30 memset(fbd, 0, sizeof fbd); 31 memset(pot, 0, sizeof pot); 32 n = read(), m = read(), insideConflict = 0; 33 for (int i=1; i<=n; i++) a[i].l = 1, a[i].r = n, b[i].l = n, b[i].r = 1; 34 for (int i=1; i<=m; i++) 35 { 36 int l = read(), r = read(), c = read(); 37 t[i].l = l, t[i].r = r, t[i].c = c; 38 if (c > n||c < 1) insideConflict = 1; 39 else{ 40 pot[c] = 1; 41 a[c].l = std::max(l, a[c].l), a[c].r = std::min(r, a[c].r); 42 b[c].l = std::min(l, b[c].l), b[c].r = std::max(r, b[c].r); 43 if (a[c].l > a[c].r) insideConflict = 1; 44 } 45 } 46 for (int i=1; i<=n; i++) 47 if (b[i].r-b[i].l+1 > i){ 48 insideConflict = 1; 49 break; 50 } 51 if (insideConflict){ 52 puts("Impossible"); 53 continue; 54 } 55 for (int i=2; i<=n; i++) 56 { 57 for (int j=1; j<=n; j++) fbd[i][j] = fbd[i-1][j]; 58 if (pot[i-1]) 59 for (int j=b[i-1].l; j<=b[i-1].r; j++) 60 fbd[i][j] = 1; 61 } 62 for (int i=1; i<=n; i++) 63 { 64 stb = 0; 65 for (int j=a[i].l; j<=a[i].r; j++) 66 if (!fbd[i][j]) stb = 1; 67 if (!stb) break; 68 stb = 0; 69 for (int j=1; j<=n; j++) 70 if (!fbd[i][j]) stb++; 71 if (stb < n-i+1){ 72 stb = 0; 73 break; 74 } 75 } 76 if (!stb) 77 puts("Impossible"); 78 else puts("Possible"); 79 } 80 return 0; 81 }
END