canvas抛物线运动轨迹

本来是想做一个贝塞尔曲线运动轨迹的

公式太复杂了，懒得算，公式在最后

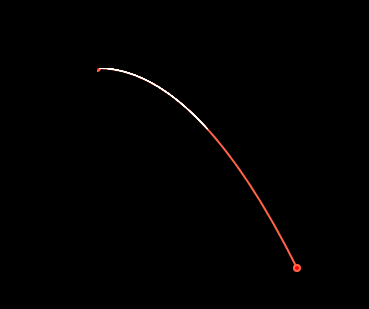
我先画了一个抛物线，我确定了两个点，起点（0,0），终点（200,200）

用坐标系可算出方程 y=-0.005x^2

现在找出终点的切线与X轴的交点，那个就是贝塞尔曲线的第二个参数，控制点

求出是（100,0）

现在重新绘制一个动态曲线，给X=X+0.1

y就是函数方程了y=0.005x^2  (注意没有负号了）

这样我们新绘制的线条就能在原来的红色线条上移动了

var oQuadraticCurveTo = document.getElementById("canvas");
var oContext = oQuadraticCurveTo.getContext("2d");
var x=2;
drawLine();
    function drawLine(){
        oContext.beginPath();
        oContext.moveTo(0,0);                       //起始点（x,y）
        oContext.quadraticCurveTo(100, 0, 200, 200);    //创建二次贝塞尔曲线
        oContext.lineWidth = 2;
        oContext.strokeStyle = "tomato";
        oContext.stroke();
        oContext.closePath(); 
    }
    function drawPoint(x,y){
        oContext.beginPath();
        oContext.arc(x, y, 3, 0, 2 * Math.PI, false);
        oContext.fillStyle="red";
        oContext.fill();
        
        oContext.stroke();
        oContext.closePath();
    }

    //画移动的线
    function drawMivie(){
        
        y=Math.pow(x,2)*0.005
        console.log(y);
        oContext.beginPath();
        oContext.moveTo(x,y); 
        x=x+0.1;
            
        if(x > 198){
            x=0;
        }else{
        //防止首位相连
        y=Math.pow(x,2)*0.005
        oContext.lineTo(x,y);
        oContext.strokeStyle = "white";
        oContext.lineWidth = 1;
        oContext.stroke();
        oContext.closePath();
        }
        

    }

    drawPoint(0,0);
    drawPoint(200,200);
    //定位到起点
    
    setInterval(function(){
            drawMivie();
        },1);
 

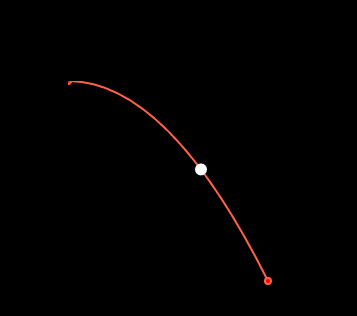
下面是一个改进版，小球沿着抛物线运动

var oQuadraticCurveTo = document.getElementById("canvas");
var oContext = oQuadraticCurveTo.getContext("2d");
var x=2; 

    function drawLine(){
        oContext.beginPath();
        oContext.moveTo(0,0);                       //起始点（x,y）
        oContext.quadraticCurveTo(100, 0, 200, 200);    //创建二次贝塞尔曲线
        oContext.lineWidth = 2;
        oContext.strokeStyle = "tomato";
        oContext.stroke();
        oContext.closePath(); 
    }
    function drawPoint(x,y){
        oContext.beginPath();
        oContext.arc(x, y, 3, 0, 2 * Math.PI, false);
        oContext.fillStyle="red";
        oContext.fill();
        
        oContext.stroke();
        oContext.closePath();

    }

    //画移动的线
    function drawMivie(){
        
        y=Math.pow(x,2)*0.005;
      
            
        if(x > 198){
            x=0;
        }else{
        //防止首位相连
　　　　　//清楚之前的图，重新绘制
        oContext.clearRect(0, 0, 500, 500);
        oContext.closePath();
        drawStatic(oContext);
        //
        x=x+1;   
        y=Math.pow(x,2)*0.005;
        //画圆球
        oContext.beginPath();
        oContext.strokeStyle = "white";
        oContext.arc(x,y,5,0,2*Math.PI,false);
        oContext.fillStyle="white";
        oContext.fill();
        oContext.stroke();
        oContext.closePath();
        }
    }
    //画静态元素,红线和两端
    function drawStatic(){
        drawLine();
        drawPoint(0,0);
        drawPoint(200,200);
    }


    setInterval(function(){
            drawMivie(oContext);
        },20);
 

公式先丢出来，万一以后真的要做复杂的曲线呢。。

用下列一组数据点P(0,1) P(1,1) P(1,0) 作为特征多边形的顶点,构造一条贝齐尔曲线,写出它的方程并作图

n个数据点构成(n-1)次贝塞尔曲线,
三个数据点构成二次贝塞尔曲线,二次贝塞尔曲线参数方程
(1 - t)^2 P0 + 2 t (1 - t) P1 + t^2 P2;
曲线起点P0,终点P2,但一般不过P1点.

代入坐标后得到:
参数方程:
x = (1 - t)^2 * 0 + 2 t (1 - t) * 1 + t^2 * 1 = 2 t (1 - t) + t^2,
y= (1 - t)^2 * 1 + 2 t (1 - t) * 1 + t^2 * 0 = (1 - t)^2 + 2 t (1 - t) ,

消去参数 t 得到:
y = -1 + 2 Sqrt[1 - x] + x.