一、红黑树的定义
【百度百科】红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
它是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。
它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
二、红黑树的特点
- 每个结点要么是红的要么是黑的。(红或黑)
- 根结点是黑的。(根黑)
- 每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。 (叶黑)
- 如果一个结点是红的,那么它的两个儿子都是黑的,不存在两个连续的红色节点。(红子黑)
- 对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。(路径下黑相同)

这五条性质约束了红黑树,才能保证红黑树的自平衡,最长路径不超过最短路径的两倍。可以通过数学证明来证明,红黑树可以将查找删除维持在对数时间内。
当我们进行插入或者删除操作时,就会对平衡造成破坏,这时候需要对树进行调整,从而重新达到平衡。所作的一切操作都是为了调整树使之符合这五条性质。
三、红黑树的操作方式
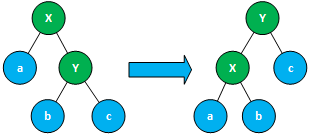
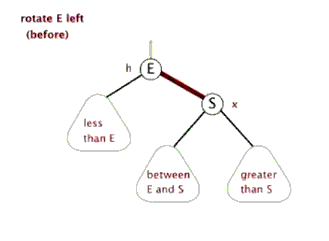
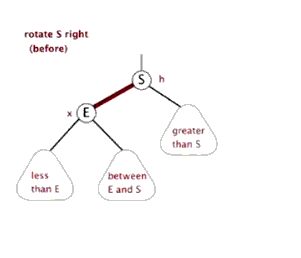
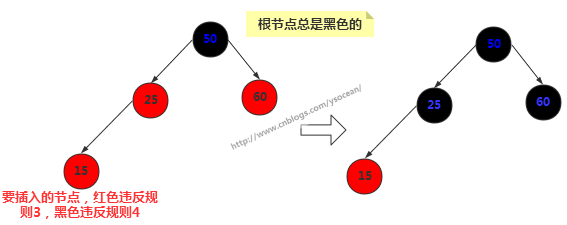
继续来深刻理解,这个很重要,在插入和删除时,红黑树的结构可能会出现不平衡的情况,此时,红-黑树主要通过三种方式对平衡进行修正,改变节点颜色、左旋和右旋。
本文不对具体的插入和删除步骤进行推导了,因为这样的文章很多,我们只讲原理,这样可能会更有意思一点。

四、红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,效率非常之高。
红黑树的查找、插入和删除时间复杂度都为O(log2N),额外的开销是每个节点的存储空间都稍微增加了一点,因为一个存储红黑树节点的颜色变量。插入和删除的时间要增加一个常数因子,因为要进行旋转,平均一次插入大约需要一次旋转,因此插入的时间复杂度还是O(log2N),(时间复杂度的计算要省略常数),但实际上比普通的二叉树是要慢的。
大多数应用中,查找的次数比插入和删除的次数多,所以应用红黑树取代普通的二叉搜索树总体上不会有太多的时间开销。而且红黑树的优点是对于有序数据的操作不会慢到O(N)的时间复杂度。
例如,Java集合中的TreeSet和TreeMap以及JDK1.8以后的HashMap在当个节点中链表长度大于8时都会用到。C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
五、总结
- 红黑树的实现其实是一个2、3、4树,只是将双节点或者三节点用红色进行了标示,如果你将红色节点放到和它父元素相同的高度,并把它和父元素看做是一个元素,你就会发现,变成了一个高度为lgN的二叉树,这个2.3.4树对红黑树很有启发意义。
- 上面的步骤其实可以不用死记硬背,是可以推导出来的,因为我们是把一个平衡但通过插入或者删除破坏了平衡的红黑树再次平衡,同过旋转让位,改变红黑颜色,使之符合那五条基本性质。比如遇到删除操作情况四的时候,我们可以把那个删除元素去除,发现左边比右边少一个黑元素,这个时候,怎么办,我们发现兄弟节点的子元素有一个红元素,操作这个不会影响那五条性质,所以我们通过变换颜色,旋转,即可让左右两边的的黑色数目一样。
- 旋转操作的目的是出让一个元素到另外的地方并且符合二叉树左小右大的性质,交换颜色的目的是为了保持红黑树的那五条性质。
- 要时刻记得 ,一切的操作都是为了保持那五条性质。
- 一定要尝试着自己推导一下插入删除规则,不然经常忘,是睡一觉起来再看就有点懵逼的那种忘。
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!

参考资料: