一、2-3-4树的定义
2-3-4树就是一种4阶的多叉树,它像红黑树一样是平衡树,可以保证在O(lgn)的时间内完成查找、插入和删除操作,容易实现,但是效率比红黑树稍差。
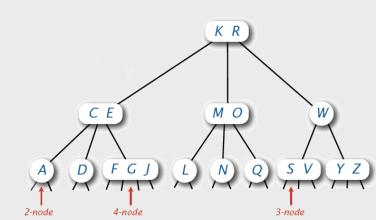
2-3-4树每个节点最多有四个字节点和三个数据项,名字中 2,3,4 的数字含义是指一个节点可能含有的子节点的个数。对于非叶节点有三种可能的情况:
- 有一个数据项的节点总是有两个子节点;
- 有二个数据项的节点总是有三个子节点;
- 有三个数据项的节点总是有四个子节点。
简而言之,非叶节点的子节点数总是比它含有的数据项多1。如果子节点个数为L,数据项个数为D,那么:L = D + 1。
二、操作
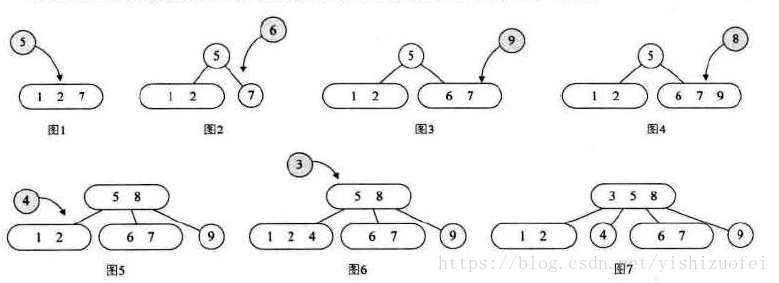
构建一个数组为{7,1,2,5,6,9,8,4,3}的2-3-4树的过程:
2-3-4树的插入:
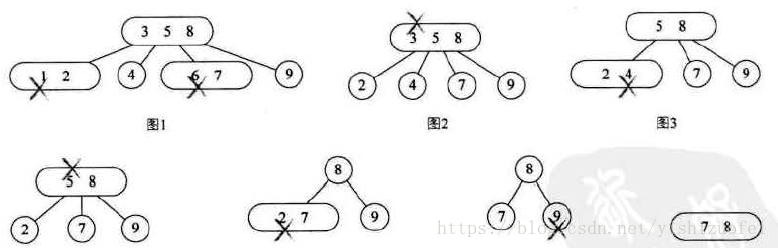
2-3-4树的删除:
三、效率
分析2-3-4树我们可以和红黑树作比较分析。红-黑树的层数(平衡二叉树)大约是log2(N+1),而2-3-4树每个节点可以最多有4个数据项,如果节点都是满的,那么高度和log4N。因此在所有节点都满的情况下,2-3-4树的高度大致是红-黑树的一半。不过他们不可能都是满的,所以2-3-4树的高度大致在log2(N+1)和log2(N+1)/2。减少2-3-4树的高度可以使它的查找时间比红-黑树的短一些。
但是另一方面,每个节点要查看的数据项就多了,这会增加查找时间。因为节点中用线性搜索来查看数据项,使得查找时间的倍数和M成正比,即每个节点数据项的平均数量。总的查找时间和M*log4N成正比。
四、2-3树
2-3树是一棵自平衡的多路查找树,它并不是一棵二叉树,具有如下性质:
- 每个节点有1个或2个key,对应的子节点为2个子节点或3个子节点;
- 所有叶子节点到根节点的长度一致;
- 每个节点的key从左到右保持了从小到大的顺序,两个key之间的子树中所有的key一定大于它的父节点的左key,小于父节点的右key。
2-3-4树只是在2-3树的基础上进行了扩展,任一节点只能是1个或2个或3个key,对应的子节点为2个子节点或3个子节点或4个子节点。
五、2-3-4树跟红黑树的转化
Java HashMap的红黑树是普通的红黑树,既可以左旋也可以右旋的。红黑树从根到叶子节点的最长路径不会超过最短路径的二倍。红黑树是黑色平衡的,即从根节点到所有叶子节点的路径,经过的黑色的节点数是相等的。 本质上来说,红黑树这个数据结构的基本思想源自于阶数为4的B树(也就是2-3-4树)。
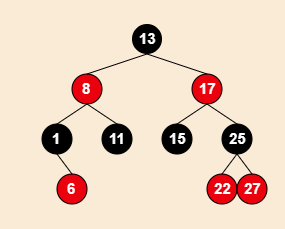 等同于
等同于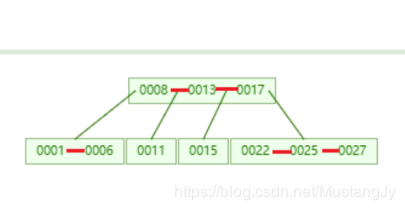
2-3-4 树是红黑树的一种等同,这意味着它们是等价的数据结构。换句话说,对于每个 2-3-4 树,都存在着至少一个数据元素是相同次序的红黑树。在 2-3-4 树上的插入和删除操作也等价于在红黑树中的颜色翻转和旋转。这使得它成为理解红黑树背后的逻辑的重要工具。
因此对于红黑树的插入等操作,可以类比4阶B树的相关操作。
1. 要将一个节点A插入,首先要将该节点的key值与树中的节点Key值相比较,最后找到一个正确的null节点位置,然后替换此null节点。此时节点A的颜色为红色。
2. if A节点父节点为黑色,那么插入过程结束,因为红色的节点不会影响红黑树的平衡
if A节点父节点为红色,那么此时要看A节点的父节点的兄弟节点,也就是A节点的叔叔节点:
if A节点没有叔叔节点,则进行红黑树的旋转操作(左旋或右旋),最后的情况是,A节点的爷爷节点的位置由A节点的父节点替换了,A节点原来的爷爷节点在旋转后成为了A节点的父节点的子节点,也就是A节点的爷爷节点成为了A节点的兄弟节点。注意,旋转的过程中,不光A节点的父节点与爷爷节点的位置要变换,两个节点的颜色也要变:
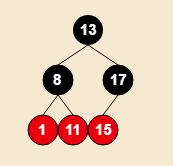 插入14 →
插入14 →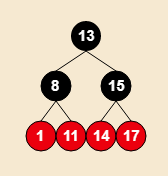 a
a
if A节点有叔叔节点(可知A节点的叔叔节点颜色应该与A节点的父节点相同,即为红色) 则将A节点的父节点和叔叔节点颜色全部置为黑色,而将A节点的爷爷节点的颜色置为红色,以保证整个红黑树仍然是黑色平衡的。 此时A节点的爷爷节点为红色,可能会导致不再满足红黑树的约束,因此要对变成红色的爷爷节点进行与插入A节点时相同的操作,来维持整个红黑树的平衡,这个过程可能是一个递归的过程。
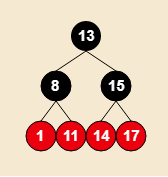 插入9 →
插入9 → 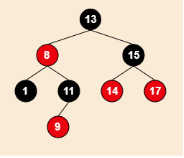
六、总结
2-3树和2-3-4树都是多路查找树。每一个结点的孩子数可以多于两个,且每一个结点处可以存储多个元素。由于它是查找树,所有元素之间存在某种特定的排序关系。
2-3-4 树是红黑树的一种等同,这意味着它们是等价的数据结构。
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!

参考资料: