多分类问题
在一个多分类问题中,因变量y有k个取值,即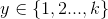 。例如在邮件分类问题中,我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类,目标值y是一个有3个取值的离散值。这是一个多分类问题,二分类模型在这里不太适用。
。例如在邮件分类问题中,我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类,目标值y是一个有3个取值的离散值。这是一个多分类问题,二分类模型在这里不太适用。
多分类问题符合多项分布。有许多算法可用于解决多分类问题,像决策树、朴素贝叶斯等。这篇文章主要讲解多分类算法中的Softmax回归(Softmax Regression)
推导思路为:首先证明多项分布属于指数分布族,这样就可以使用广义线性模型来拟合这个多项分布,由广义线性模型推导出的目标函数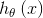 即为Softmax回归的分类模型。
即为Softmax回归的分类模型。
证明多项分布属于指数分布族
多分类模型的输出结果为该样本属于k个类别的概率,从这k个概率中我们选择最优的概率对应的类别(通常选概率最大的类别),作为该样本的预测类别。这k个概率用k个变量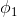 ,
,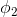 …,
…,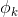 表示。这个k变量和为1,即满足:
表示。这个k变量和为1,即满足:
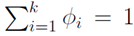
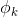 可以用前k-1个变量来表示,即:
可以用前k-1个变量来表示,即:
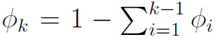
使用广义线性模型拟合这个多分类问题,首先要验证这个多项分布是否符合一个指数分布族。定义T(y)为:
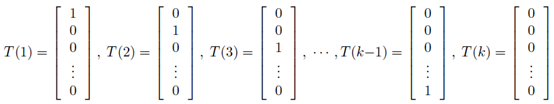
在这里,统计分量T(y)并没有像之前那样定义为T(y)=y,因为T(y)不是一个数值,而是一个k-1维的向量。使用符号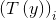 表示向量T(y)的第i个元素。
表示向量T(y)的第i个元素。
在这里引入一个新符号: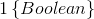 ,如果括号内为true则这个符号取1,反之取0,即
,如果括号内为true则这个符号取1,反之取0,即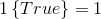 ,
,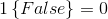 。所以,T(y)与y的关系就可以表示为
。所以,T(y)与y的关系就可以表示为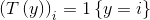
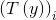 与
与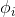 关系为:
关系为:
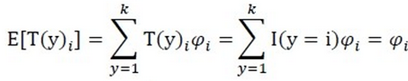
即:
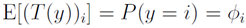
多项分布表达式转化为指数分布族表达式过程如下:
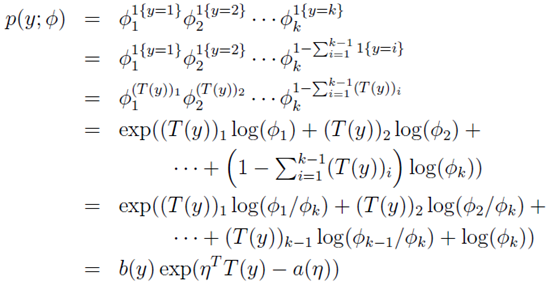
其中:
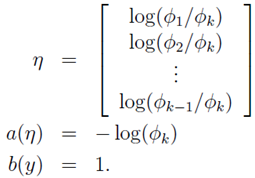
变换过程:
第一步: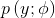 取值为
取值为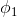 ,
,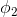 …,
…,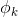 中的一个,取决于y的取值。当y=i时,这一步可以理解为
中的一个,取决于y的取值。当y=i时,这一步可以理解为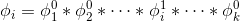
第二步:消去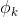
第三步:根据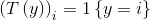
第四、五步:转换为广义线性模型的表达格式。
多项分布表达式可以表示为指数分布族表达式的格式,所以它属于指数分布族,那么就可以用广义线性模型来拟合这个多项式分布模型。
Softmax函数(Softmax Function)
在使用广义线性模型拟合这个多项式分布模型之前,需要先推导一个函数,这个函数在广义线性模型的目标函数中会用到。这个函数称为Softmax函数(Softmax Function)。
由η表达式可得:

这是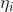 关于
关于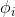 的表达式,把它转化为
的表达式,把它转化为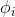 关于
关于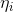 的表达式过程为:
的表达式过程为:
为了方便,令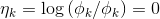 ,那么
,那么
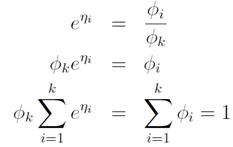
因为:
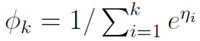
所以:
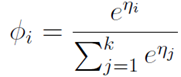
这个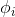 关于
关于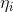 的的函数称为Softmax函数(Softmax Function)。
的的函数称为Softmax函数(Softmax Function)。
使用广义线性构建模型
根据广义线性模型的假设3:
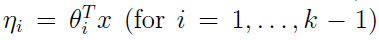
θ是模型中的参数,为了符号上的方便我们定义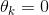 ,所以
,所以
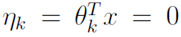
所以模型在给定x的条件下y的分布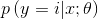 为:
为:
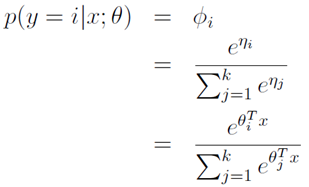
上面的表达式求解的是在y=i时的概率。在Softmax回归这个广义线性模型中,目标函数是:
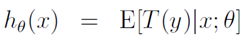
Softmax回归目标函数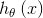 的输出是k个概率,即
的输出是k个概率,即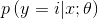 其中i=1,2,…,k(虽然输出的是k-1个值,但是第k个值
其中i=1,2,…,k(虽然输出的是k-1个值,但是第k个值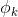 可以由
可以由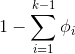 求出),求解了这个目标函数,我们就构造出了分类模型。
求出),求解了这个目标函数,我们就构造出了分类模型。
目标函数推导过程如下:

现在求解目标函数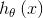 还差最后一步:参数拟合的问题。跟我们之前的参数拟合方法类似,我们有m个训练样本,θ的似然函数为:
还差最后一步:参数拟合的问题。跟我们之前的参数拟合方法类似,我们有m个训练样本,θ的似然函数为:
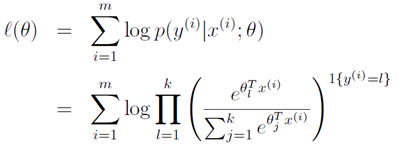
最大化似然函数来求解最优的参数θ,可以使用梯度上升或者牛顿方法。
求解了最优的参数θ后,就可以使用目标函数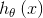 进行分类。使用函数
进行分类。使用函数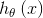 进行多分类的方式就叫Softmax回归(Softmax Regression)
进行多分类的方式就叫Softmax回归(Softmax Regression)