前言
归并排序(Merge Sort)是利用“归并”技术来进行排序。归并是指将若干个已排序的子文件合并成一个有序的文件。
一、两路归并排序算法
1、算法基本思路
设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上:R[low..m],R[m+1…high],先将它们合并到一个局部的暂存向量R1(相当于输出堆)中,待合并完成后将R1复制回R[low…high]中。
2、两路归并排序算法核心
归并排序的算法思想是分而治之(divide-conquer),每个递归过程分为三个步骤:
1)分解:把待排序的n个元素的序列分解成两个子序列,每个子序列包括n/2个元素;
2)治理:对每个子序列分别调用归并排序(MergeSort),进行归并操作;
3)合并:合并两个排好序的子序列,生成排序结果。
3、两路归并排序的示例
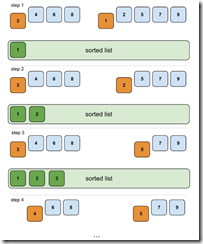
归并排序是一个基于分治法的比较排序算法。目前看来还不错,那么当我们有一个非常大的列表需要排序。显然,如果我们将列表分成两个子列表,然后排序他们会更好些。如果等分以后还是太大,那就继续分割,知道我们可以很简单排序为止,如下图。。
上图描述了在算法中的某些步骤,我们已经得到两个排好序的列表,接着要做的就是巧妙地合并它们。然而,这也不是特别难。我们可以比较两个列表的第一个元素,将其中较小的元素取出放在一个新的列表中(这样得到的列表一定是有序的列表)。
4、两路归并排序算法的实现
/**功能:归并排序用分治法对arr[low..high]进行二路归并排序*/void MergeSort(int arr[],int low, int high){int mid;if (low<high) // 保证区间长度大于1{mid = (low+high)/2; // 分解MergeSort(arr,low,mid); // 递归地对arr[low..mid]排序MergeSort(arr,mid+1,high); // 递归地对arr[mid+1...high]排序Merge(arr,low,mid,high); // 组合,将两个有序区归并为一个有序区}}
/**功能:合并两个序列,组成新的一个有序序列思路:1、使用临时序列始终保持两个序列中最小的值2、将临时序列的值赋给组合的这个序列*/void Merge(int arr[], int start, int mid, int end){int i,j,m,n; // 记录两个区间的起始于结束位置int k; // 为临时存储这两个区间的开始位置int *temp; // 临时存储合并两个区间的值i = start; j = mid + 1; // 两个区间的起始位置m = mid; n = end; // 两个区间的结束位置k = 0; temp = NULL;temp = new int[end-start+1];if (NULL == temp){cout << "内存分配失败!" << endl;exit(-1);}while (i<=m && j<=n) // 存储两个区间公共长度的最小值{if (arr[i]<=arr[j]){temp[k++] = arr[i++];}elsetemp[k++] = arr[j++];}while (i<=m) // 存储第一个区间剩下的最小值(如果还剩下的话){temp[k++] = arr[i++];}while (j<=n) // 存储第二个区间剩下的最小值(如果还剩下的话){temp[k++] = arr[j++];}for (i=0; i<k; i++) // 将临时存储的值重新赋给输入数组{arr[start+i] = temp[i]; // start的值不一定是0,因此在赋值时不能省略}delete []temp; // 释放内存temp = NULL;}
5、归并排序算法的性能分析
归并排序是一种稳定的排序,对于长度为n的文件,需进行趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。
归并排序需要一个辅助向量来暂存两个有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。