语音信号处理要达到的一个目标,就是弄清楚语音中各个频率成分的分布。做这件事情的数学工具是傅里叶变换,但傅里叶变换要求输入信号是平稳的,而语音在宏观上来看是不平稳的(波形很不均匀)。语音信号特征是随时间变化而变化的,是一个非平稳的随机过程。但从微观上看,虽然语音信号具有时变特征,但在一个短时间内其特征基本保持不变(肌肉运动有惯性,从一个状态到到另一个状态的转变不可能瞬间完成),我们称之为语音的“短时平稳性”。所有对语音的分析和处理必须建立在“短时”的基础上,即对语音信号采用分段处理,每一段成为一帧。通常语音在10~30ms之内是保持相对平稳的,所以帧长一般取为10~30ms,截取后的每一帧信号,便可以做傅里叶变换了。
下图中这段语音的前三分之一和后三分之二明显不一样,所以整体来看语音信号不平稳。红框框出的部分是一帧,在这一帧内部的信号可以看成平稳的。

取出来的一帧信号,在做傅里叶变换之前,要先进行“加窗”的操作,即与一个“窗函数”相乘,如下图所示:

加窗的目的是让一帧信号的幅度在两端渐变到 0。渐变对傅里叶变换有好处,可以提高变换结果(即频谱)的分辨率。加窗的代价是一帧信号两端的部分被削弱了,没有像中央的部分那样得到重视。弥补的办法是,帧不要背靠背地截取,而是相互重叠一部分。相邻两帧的起始位置的时间差叫做帧移,常见的取法是取为帧长的一半,或者固定取为 10 毫秒。否则,由于帧与帧连接处的信号会因为加窗而被弱化,这部分的信息就丢失了。
对一帧信号做傅里叶变换,得到的结果叫频谱(一般只保留幅度谱,丢弃相位谱),它就是下图中的蓝线:

图中的横轴是频率,纵轴是幅度。频谱上就能看出这帧语音在 480 和 580 赫兹附近的能量比较强。语音的频谱,常常呈现出“精细结构(音高 pitch)”和“包络(音素)”两种模式。“精细结构”就是蓝线上的一个个小峰,它们在横轴上的间距就是基频,它体现了语音的音高——峰越稀疏,基频越高,音高也越高。“包络”则是连接这些小峰峰顶的平滑曲线(红线),它代表了口型,即发的是哪个音。包络上的峰叫共振峰,图中能看出四个,分别在 500、1700、2450、3800 赫兹附近。有经验的人,根据共振峰的位置,就能看出发的是什么音。
接下来把频谱与下图中每个三角形相乘并积分,求出频谱在每一个三角形下的能量。
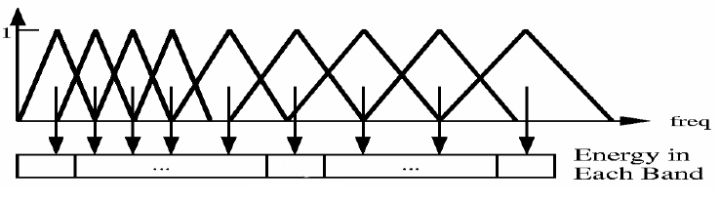
这一步有以下作用:
2) 频谱有包络和精细结构,分别对应音色与音高。对于语音识别来讲,音色是主要的有用信息,音高一般没有用。在每个三角形内积分,就可以消除精细结构,只保留音色的信息。
将上一步的结果取对数。简单理解,它是对纵轴的放缩,可以放大低能量处的能量差异。求倒谱时这一步仍然用的是傅里叶变换。计算MFCC时使用的离散余弦变换(discrete cosine transform,DCT)是傅里叶变换的一个变种,好处是结果是实数,没有虚部。DCT还有一个特点是,对于一般的语音信号,这一步的结果的前几个系数特别大,后面的系数比较小,可以忽略。上面说了一般取40个三角形,所以DCT的结果也是40个点;实际中,一般仅保留前12~20个,这就进一步压缩了数据。
上面整个过程的结果,就把一帧语音信号用一个12~20维向量简洁地表示了出来;一整段语音信号,就被表示为这种向量的一个序列。语音识别中下面要做的事情,就是对这些向量及它们的序列进行建模了。
参考: